Poprzednia Następna (dział 4)

Szufladkowa Dirichleta
Definicja
Zasada szufladkowa Dirichleta – twierdzenie mówiące, że jeżeli m przedmiotów włożymy do n różnych szufladek, przy czym m > n, to co najmniej w jednej szufladce znajdą się co najmniej dwa przedmioty.
Sformułowanie twierdzenia przypisuje się Dirichletowi, a w bardziej formalnym języku można wysłowić je na przykład tak:

jeżeli zbiór X liczy n elementów i X=X₁∪ X₂∪...∪ X_k i n>k, to któryś ze zbiorów X_i musi liczyć przynajmniej dwa elementy.

Inna wersja formalna brzmi następująco:

jeżeli zbiór X liczy n elementów, zbiór Y – m elementów i n>m, to nie istnieje funkcja różnowartościowa ze zbioru X do zbioru Y.

Wydaje się, że ta oczywista obserwacja nie może mieć poważnych zastosowań, ale jest akurat odwrotnie. Zasada szufladkowa wykorzystywana w dowodach wielu głębokich twierdzeń matematycznych i często samo zauważenie, że można ją zastosować jest kluczem do rozwiązania problemu.

Przykłady

• W oparciu o zasadę szufladkową nietrudno wykazać, że wśród mieszkańców Warszawy co najmniej dwie osoby mają tę samą liczbę włosów na głowie. Rzeczywiście, liczba włosów na głowie człowieka nie przekracza 500 000, natomiast liczba mieszkańców Warszawy przekracza 1 000 000. Weźmy 500 000 szufladek ponumerowanych kolejnymi liczbami naturalnymi od 1 do 500 000 i wkładajmy do szufladki o danym numerze osoby, które mają taką liczbę włosów na głowie, jak numer szufladki. Ponieważ osób jest 1 000 000, a szufladek 500 000, z naszej zasady wynika, że w jednej szufladce muszą znaleźć się co najmniej dwie osoby (a nawet co najmniej trzy).
• Analogicznie można wykazać, że w grupie 20 osób muszą być co najmniej dwie, które urodziły się w tym samym miesiącu. Weźmy mianowicie 12 szufladek z nazwami miesięcy i wkładajmy do nich osoby, które urodziły się w danym miesiącu. Ponieważ osób jest 20, a szufladek 12, w jednej z nich muszą być co najmniej dwie osoby.
• Następny przykład dotyczy spraw nieco "poważniejszych" – w oparciu o zasadę szufladkową uzasadnimy, że wśród kolejnych potęg liczby 7: 7, 7², 7³, 7⁴, ... istnieje taka, której zapis dziesiętny kończy się na 001.
  Rozważmy mianowicie 1000 kolejnych liczb tej postaci: 7, 7², 7³, 7⁴, ..., 71000 i przyjrzyjmy się ich resztom z dzielenia przez 1000. Żadna z reszt nie jest równa 0 (bo żadna z wypisanych liczb nie dzieli się przez 1000). Wkładajmy do jednej szufladki dwie liczby wtedy i tylko wtedy, gdy z dzielenia przez 1000 dają tę samą resztę – ponieważ różnych reszt jest co najwyżej 999, a liczb 1000, co najmniej dwie liczby muszą znaleźć się w tej samej szufladce, co oznacza, że ich różnica jest podzielna przez 1000. Niech będą to liczby 7^k i 7^l, gdzie k > l – ich różnica jest równa 7^k - 7^l = 7^l(7^k-l - 1) i dzieli się przez 1000. Liczba 7^l oraz 1000 nie mają wspólnych dzielników (więc się nie skrócą), a zatem musi przez 1000 dzielić się liczba 7^k-l - 1. Oznacza to, że jej zapis dziesiętny kończy się co najmniej trzema zerami: 7^k-l-1=...000, a stąd natychmiast mamy, że 7^k-l=...000+1=...001.
• Pomalujmy płaszczyznę w dowolny sposób na dwa kolory: biały i czarny. To znaczy przypiszmy każdemu punktowi płaszczyzny jeden z tych dwu kolorów. Na takiej płaszczyźnie istnieje prostokąt, który ma wszystkie wierzchołki tego samego koloru. Bardziej formalnie: wyznaczmy na płaszczyźnie dowolny zbiór B oraz jego dopełnienie C=B'; istnieje prostokąt, którego wszystkie wierzchołki należą do B, albo taki, którego wszystkie wierzchołki należą do C.
• Zbierzmy razem N osób (N≥2). Być może niektórzy z nich mają wśród zebranych znajomych. Być może każdy ma w niej kogoś znajomego; a może żaden nie ma. Wśród tych N osób są dwie osoby, które mają wśród zebranych tyle samo znajomych. Bardziej formalnie: w każdym grafie skończonym o co najmniej dwu węzłach istnieją dwa węzły o tym samym stopniu.

Włączeń i wyłączeń
Definicja
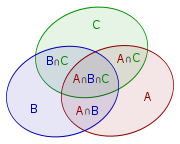Zasada włączeń i wyłączeń - reguła kombinatoryczna, pozwalająca na określenie liczby elementów skończonej sumy mnogościowej skończonych zbiorów. Autorstwo zasady przypisywane jest zazwyczaj Abrahamowi de Moivre, chociaż bywa nazywana od nazwisk matematyków, Jamesa Josepha Sylvestera oraz Henriego Poincaré.
Twierdzenie
Niech A₁,A₂,...,A_n będą dowolnymi zbiorami zaś i,j,k∈{1,...,n}. Wówczas

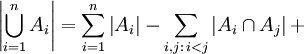
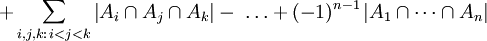
gdzie |A_k| oznacza moc zbioru A_k
Dowód
Niech element a należy dokładnie do m spośród zbiorów A₁,A₂,...,A_n. W sumie mnogościowej 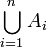jest on liczony jeden raz. W wyrażeniu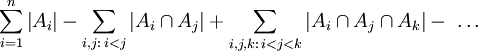

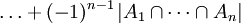
ilość zliczeń pojedynczego elementu jest równa:

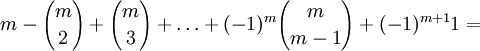
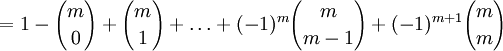
bowiem występuje on w m zbiorach spośród A1,A2,...,An, 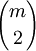, zbiorach spośród A_i ∩ A_j, 1 ≤ i ≤ j ≤ n itd.
Na mocy rozwinięcia Newtona wyrażenie to jest równe 1 - (1 - 1)^m = 1 - 0 = 1, co dowodzi poprawności zasady włączeń i wyłączeń, bowiem element został policzony jeden raz.
Przykłady

• Dla trzech zbiorów skończonych A₁,A₂,A₃ liczba elementów ich sumy wyraża się wzorem:
  
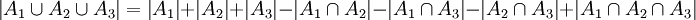
  Wzór zapewnia, że elementy znajdujące się jednocześnie w kilku spośród zbiorów A₁,A₂,...,A_n liczone są dokładnie raz.
• Zbadano 50 samochodów, wykorzystując testy na poziom zawartości 3 grup zanieczyszczeń NO_x, HC oraz CO.
  1 samochód nie spełnia żadnej normy, 3 samochody przekroczyły poziom NO_x i HC, 2 miały za wysoki poziom NO_x i CO, 1 samochód przekroczył poziom HC i CO, 6 miało za wysoki poziom NO_x, 4 przekroczyło poziom HC, a 3 CO.
  Ile samochodów spełnia wszystkie testowane normy?
  A₁- zbiór samochodów o przekroczonym poziomie NO_x;
  A₂- zbiór samochodów o przekroczonym poziomie HC;
  A₃- zbiór samochodów o przekroczonym poziomie CO.
  |A₁|=6, |A₂|=4, |A₃|=3.
  |A₁∩A₂|=3, |A₁∩A₃|=2, |A₂∩A₃|=1, |A₁∩A₂∩A₃|=1;
  zbiór samochodów, które nie spełnieją co najmniej 1 z norm= A₁∪A₂∪A₃
  |A₁∪A₂∪A₃|=6+4+3-3-2-1+1=8;
  zbiór tych, które spełniają= 50-8= 42.

Poprzednia Następna (dział 4)