Algorytmy grafowe
A*
- Definicja Algorytm A* – algorytm przeszukiwania grafu, odnajdujący najkrótszą ścieżkę pomiędzy dwoma danymi wierzchołkami grafu (lub dokładniej, między wierzchołkiem początkowym a dowolnym z wierzchołków docelowych). Wykorzystuje heurystykę. Przy przeszukiwaniu grafu najpierw sprawdza najbardziej obiecujące, jeszcze nie odkryte wierzchołki.
- Działanie algorytmu Algorytm A* począwszy od wierzchołka początkowego tworzy ścieżkę za każdym razem wybierając wierzchołek x z dostępnych w danym kroku niezbadanych wierzchołków tak, by minimalizować funkcję f(x) zdefiniowaną:
- Przykład ilustrujący działanie Oto przykład działania algorytmu A* dla grafu, którego wierzchołkami są miasta, wagami krawędzi odległości drogowe, a heurystyka h(x) jest odległością w linii prostej. Przykład pokazuje prostą sytuację, w której A* wykona nawrót ze względu na niesłuszne przewidywania heurystyki.
- Algorytm A* w pseudokodzie Open set i closed set nie mają nic wspólnego ze zbiorami otwartymi i domkniętymi w znaczeniu topologicznym.
- Cechy algorytmu A* A* jest kompletny - w każdym przypadku znajdzie optymalną drogę i zakończy działanie, jeśli taka droga istnieje. Heurystyka h jest dopuszczalna, jeśli nigdy nie zawyża wartości wagi na ścieżce między dowolnymi dwoma wierzchołkami, czyli dla wierzchołków x i y:
- Dlaczego A* jest dopuszczalny oraz optymalny obliczeniowo? Zakładając iż używana w algorytmie heurystyka jest dopuszczalna, możemy stwierdzić iż A* jest dopuszczalny (ang. admissible). Oznacza to, iż zawsze poda nam prawidłowe rozwiązanie, jeżeli takowe istnieje. Co więcej algorytm ten podczas działania przeszukuje mniej węzłow niż jakikolwiek inny dopuszczalny algorytm przeszukiwania z taką samą heurystyką. Dzieje się tak, gdyż A* tworzy “optymistyczne” oszacowanie kosztu ścieżki przez każdy węzeł, który bierze pod uwagę - optymistyczny w sensie, iż prawdziwy koszt ścieżki przez dany węzeł do węzła końcowego będzie co najmniej tak duży jak oszacowanie.
- Złożoność Złożoność czasowa algorytmu A* zależy od zastosowanej heurystyki. W najgorszym przypadku liczba przeszukanych węzłów rośnie wykładniczo w stosunku do długości rozwiązania (najkrótszej ścieżki), natomiast rośnie już tylko wielomianowo, jeśli funkcja heurystyki h spełnia następujący warunek:
- Zastosowania wykraczające poza teorię grafów Algorytm A* w parsowaniu - znaczne zmniejszenie złożoności parsowania Probabilistycznych gramatyk bezkontekstowych
Algorytm opisany pierwotnie w 1968 roku przez Petera Harta, Nilsa Nilssona oraz Bertram Raphael. W ich pracy naukowej został nazwany algorytmem A. Ponieważ jego użycie daje optymalne zachowanie dla danej heurystyki, nazwano go A*.
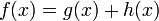
gdzie:
- g(x) - droga pomiędzy wierzchołkiem początkowym a x. Dokładniej: suma wag krawędzi jakie już należą do ścieżki plus waga krawędzi łączącej aktualny węzeł z x.
- h(x) - przewidywana przez heurystykę droga od x do wierzchołka docelowego.
W każdym kroku algorytm dołącza do ścieżki wierzchołek o najniższym współczynniku f. Kończy w momencie natrafienia na wierzchołek będący wierzchołkiem docelowym (lub jednym z wierzchołków docelowych)
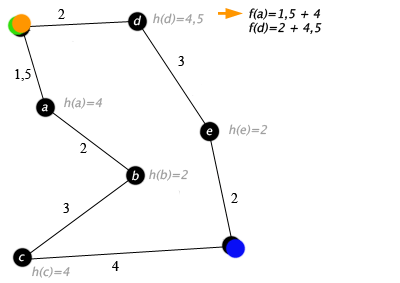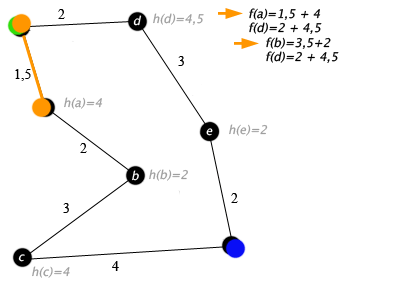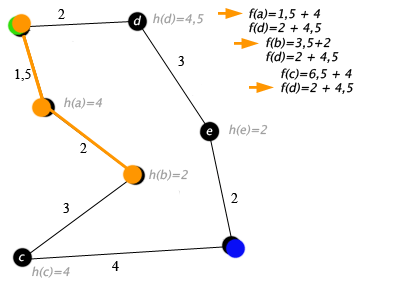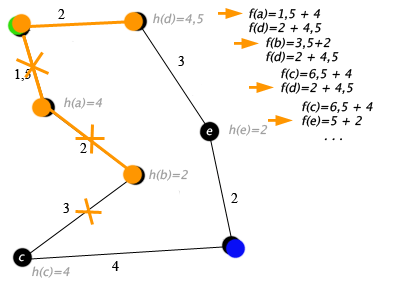
zielony - wierzchołek początkowy, niebieski - wierzchołek docelowy.
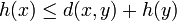
gdzie d(x,y) oznacza faktyczną odległość między wierzchołkami x i y
Spełnienie tego warunku gwarantuje poprawność decyzji podejmowanych przez algorytm w oparciu o heurystykę, ponieważ nie zajdzie sytuacja, w której h(x) dla pewnego x będzie większe niż faktyczna długość ścieżki z x do wierzchołka docelowego. Nie spełnienie warunku oznacza, że algorytm mógłby wskazać nieoptymalną ścieżkę jeśli dla pewnego węzła y w optymalnej ścieżce h(y) byłoby zawyżone. Algorytm A* jest optymalny dla danej heurystyki, co znaczy, że nie istnieje inny algorytm, który z pomocą tej samej heurystyki odwiedziłby mniej wierzchołków niż A*.
Przypadki graniczne - Istnieją bardziej znane algorytmy grafowe, które można osiągnąć używając A* charakterystycznym grafie i/lub z charakterystyczną heurystyką:
- Przeszukiwanie w głąb
- Przeszukiwanie wszerz
- Algorytm Dijkstry -
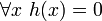
Kiedy A* kończy przeszukiwanie, ma, z definicji, znalezioną ścieżkę, której koszt jest mniejszy niż szacowany koszt jakiejkolwiek innej ścieżki (innej, czyli przechodzącej co najmniej przez jeden węzeł niewchodzący w skład znalezionej ścieżki). Ale z faktu, iż te oszacowania są optymistyczne, algorytm A* może bezpiecznie zignorować te inne ścieżki. Innymi słowy, A* nigdy nie “przeoczy” ścieżki o niższym koszcie i dlatego jest dopuszczalny.
Przypuśćmy teraz, że jakiś inny algorytm B kończy swoje przeszukiwanie ze ścieżką, której koszt jest nie mniejszy niż szacowany koszt ścieżki przez jakiś węzeł X nie wchodzący w skład znalezionej ścieżki. Algorytm B nie może wykluczyć, bazując na informacjach wynikających z posiadanej heurystyki, możliwości, że ścieżka przez węzeł X może mieć niższy koszt niż znaleziona ścieżka. Z tego wynika, iż jeżeli B bierze pod uwagę mniejszą ilość węzłów niż A*, to B nie jest dopuszczalny. W związku z tym można stwierdzić, że A* bierze pod uwagę najmniejszą liczbę węzłów ze wszystkich dopuszczalnych algorytmów przeszukiwań, oczywiście pod warunkiem, że algorytmy te nie używają heurystyk dających bardziej dokładne oszacowania.
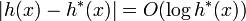
gdzie h * jest optymalną heurystyką, czyli zawsze podaje dokładny, rzeczywisty koszt ścieżki z x do węzła końcowego. Innymi słowy, błąd funkcji h nie powinien rosnąć szybciej niż logarytm “dokładnej heurystyki” h * .
Bardziej problematyczne niż koszt czasowy, jest użycie pamięci przez A*. W najgorszym przypadku, algorytm musi zapamiętać liczbę węzłów, która rośnie wykładniczo w stosunku do długości rozwiązania. Kilka wariantów algorytmu A* zostało stworzonych, by rozwiązać ten problem. Niektóre z nich to: IDA* (ang. iterative deepening A*), MA* (ang. memory-bounded A*), SMA* (ang. simplified memory-bounded A*) oraz RBFS (ang. recursive best-first search).
- Definicja Algorytm Bellmana-Forda rozwiązuje problem najkrótszej ścieżki, tj. pozwala znaleźć ścieżkę o najmniejszej wadze pomiędzy dwoma wierzchołkami w grafie ważonym. Idea algorytmu opiera się na metodzie relaksacji (dokładniej następuje relaksacja V - 1 razy każdej z krawędzi).
- Zapis w pseudokodzie Dla grafu G, funkcji wagowej w i wierzchołka s otrzymamy tablicę d[u] odległości każdego wierzchołka grafu od wierzchołka s.
W odróżnieniu od algorytmu Dijkstry, poprawność algorytmu Bellmana-Forda nie opiera się na założeniu, że wagi w grafie są nieujemne (nie może jednak występować cykl o łącznej ujemnej wadze osiągalny ze źródła). Za tę ogólność płaci się jednak wyższą złożonością czasową. Działa on w czasie O(V*E).
Uwaga:
Dla grafów z wagami o nieujemnych wartościach lepiej jest stosować Algorytm Dijkstry.
Po znalezieniu najkrótszej odległości między wierzchołkami możemy znaleźć drogę łączącą te wierzchołki za pomocą algorytmu konstrukcji drogi.
- Definicja Algorytm Dijkstry, opracowany przez holenderskiego informatyka Edsgera Dijkstrę, służy do znajdowania najkrótszej ścieżki z pojedynczego źródła w grafie o nieujemnych wagach krawędzi. Jest często używany w trasowaniu.
- Algorytm Przez s oznaczamy wierzchołek źródłowy, w(i,j) to waga krawędzi (i,j) w grafie.
- Pseudokod
- Dowód poprawności Oznaczmy przez S zbiór wierzchołków, które zostały już zdjęte z kolejki. Dowód opiera się na następujących dwóch faktach (niezmiennikach), prawdziwych przez cały czas trwania algorytmu:
- Złożoność Złożoność obliczeniowa algorytmu Dijkstry zależy od liczby V wierzchołków i E krawędzi grafu. O rzędzie złożoności decyduje implementacja kolejki priorytetowej:
- Problemy i algorytmy pokrewne Algorytm Dijkstry nie działa, jeśli w grafie występują krawędzie z ujemnymi wagami – w tym wypadku używa się wolniejszego, lecz bardziej ogólnego algorytmu Bellmana-Forda. Jeśli graf nie jest ważony (wszystkie wagi mają wielkość 1), zamiast algorytmu Dijkstry wystarczy algorytm przeszukiwania grafu wszerz. Algorytm A* jest pewnym uogólnieniem algorytmu Dijkstry, które pozwala przeszukiwać tylko część grafu, jednak wymaga dodatkowej wstępnej informacji (heurystyki) o odległościach wierzchołków.
Mając dany graf z wyróżnionym wierzchołkiem (źródłem) algorytm znajduje odległości od źródła do wszystkich pozostałych wierzchołków. Łatwo zmodyfikować go tak, aby szukał wyłącznie ścieżki do jednego ustalonego wierzchołka, po prostu przerywając działanie w momencie dojścia do wierzchołka docelowego.
Algorytm Dijkstry jest przykładem algorytmu zachłannego.
1. Stwórz tablicę d odległości od źródła dla wszystkich wierzchołków grafu. Na początku d[s] = 0, zaś d[v] = nieskończoność dla wszystkich pozostałych wierzchołków.
2. Utwórz kolejkę priorytetową Q wszystkich wierzchołków grafu. Priorytetem kolejki jest aktualnie wyliczona odległość od wierzchołka źródłowego s.
3. Dopóki kolejka nie jest pusta:
- Usuń z kolejki wierzchołek u o najniższym priorytecie (wierzchołek najbliższy źródła, który nie został jeszcze rozważony)
- Dla każdego sąsiada v wierzchołka u dokonaj relaksacji poprzez u: jeśli d[u] + w(u,v) < d[v] (poprzez u da się dojść do v szybciej niż dotychczasową ścieżką), to d[v]: = d[u] + w(u,v).
Na końcu tablica d zawiera najkrótsze odległości do wszystkich wierzchołków.
Dodatkowo, możemy w tablicy poprzednik przechowywać dla każdego wierzchołka numer jego bezpośredniego poprzednika na najkrótszej ścieżce, co pozwoli na odtworzenie pełnej ścieżki od źródła do każdego wierzchołka – przy każdej relaksacji w ostatnim punkcie, u staje się poprzednikiem v.
1. Dla każdego wierzchołka
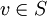, liczba d[v] jest długością najkrótszej ścieżki od s do v.2. Dla każdego wierzchołka
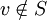, d[v] jest długością najkrótszej krawędzi do v prowadzącej tylko przez wierzchołki z S.
Na początku oba fakty są oczywiste (S jest zbiorem pustym). Przy zdejmowaniu wierzchołka u z kolejki wiemy, na podstawie faktu 2, że nie da się do niego dojść żadną krótszą drogą przez wierzchołki z S. Z drugiej strony, ponieważ u ma najniższy priorytet, przejście przez jakikolwiek inny wierzchołek spoza S dałoby od razu co najmniej tak samo długą ścieżkę. A zatem dołączając wierzchołek u do S zachowujemy prawdziwość faktu 1. Następnie musimy uwzględnić fakt, że najkrótsza ścieżka do jakiegoś wierzchołka v po wierzchołkach z nowego zbioru S może teraz zawierać wierzchołek u. Ale wtedy musi on być ostatnim na niej wierzchołkiem (do każdego innego dałoby się dojść krócej nie używając u), a zatem jej długość równa jest d[u] + w(u,v) i zostanie prawidłowo obliczona w następnym kroku algorytmu.
- wykorzystując "naiwną" implementację poprzez zwykłą tablicę, otrzymujemy algorytm o złożoności O(V²)
- w implementacji kolejki poprzez kopiec, złożoność wynosi O(ElogV)
- po zastąpieniu zwykłego kopca kopcem Fibonacciego, złożoność zmniejsza się do O(E + VlogV)
Pierwszy wariant jest optymalny dla grafów gęstych (czyli jeśli E = Θ(V²)), drugi jest szybszy dla grafów rzadkich (E = Θ(V)), trzeci jest bardzo rzadko używany ze względu na duży stopień skomplikowania i niewielki w porównaniu z nim zysk czasowy.
Algorytm Prima znajdowania minimalnego drzewa rozpinającego oparty jest o bardzo podobny pomysł, co algorytm Dijkstry.
- Definicja Jest to algorytm pozwalający na odszukanie cyklu Eulera w grafie eulerowskim.
- Poszukiwanie ścieżki Eulera w grafie Przypuśćmy, że dany jest graf G i że G jest grafem eulerowskim. Chcemy teraz znaleźć cykl Eulera wiodący od określonego wierzchołka v.
- Pseudokog algorytmu Przyjmijmy, że algorytm zwraca wynik wpisując do pewnej sekwencyjnej struktury kolejne wierzchołki w odwrotnej kolejności, niż znajdują się na ścieżce. Struktura ta może być całkowicie dowolna i jest określana jako po prostu „rozwiązanie”. Przyjmijmy również, że dysponujemy stosem S, na którym można wykonywać operacje PUSH i POP oraz sprawdzać, czy stos jest pusty, funkcją EMPTY. Jeśli zadany graf G posiada konstruktor kopiujący, początkowym wierzchołkiem ścieżki jest v, a końcowym w, wówczas działanie algorytmu można przedstawić w następujących krokach:
- Dowód poprawności algorytmu Załóżmy, że poszukujemy cyklu Eulera w grafie eulerowskim G. Wówczas wierzchołek końcowy w jest tożsamy z wierzchołkiem początkowym v, graf G jest spójny i stopień każdego wierzchołka jest liczbą parzystą. Poprawność algorytmu wykażemy używając indukcji względem liczby krawędzi.
Algorytm Fleury’ego konstruuje oczywiście szlak. Co więcej prawdziwe jest twierdzenie:
„Jeżeli G jest grafem eulerowskim to dowolny szlak w G skonstruowany przy pomocy algorytmu Fleury’ego jest obchodem Eulera grafu G.”
Można przemierzać ścieżkę cykliczną usuwając napotkane krawędzie i gromadząc na stosie napotkane wierzchołki, dzięki czemu:
1. Możemy zawrócić po ścieżce i wydrukować jej krawędzie.
2. Możemy sprawdzić, czy dla każdego wierzchołka istnieją ścieżki prowadzące z innych stron (które można połączyć w jedną ścieżkę).
Zwróćmy uwagę na fakt, że algorytm wymaga stworzenia kopii lokalnej grafu, aby móc z niej usunąć poszukiwaną ścieżkę. Dlatego też jest niezwykle ważne, czy klasa definiująca abstrakcyjny typ danych graf posiada konstruktor kopiujący oraz czy tworzy on kompletną i odseparowaną kopię grafu. W implementacji algorytmu przyjęto, że tak jest. W przeciwnym wypadku po zakończeniu działania algorytmu należałoby jeszcze raz przemierzyć ścieżkę Eulera, ponownie dodając do grafu wszystkie jej krawędzie.
Algorytm rozpoczyna się od stworzenia lokalnej kopii G’ grafu G i dodania końcowego wierzchołka do odwrotnej listy wierzchołków, które należy kolejno odwiedzać, aby odnaleźć cykl Eulera w grafie G.
W krokach 4 – 8 algorytmu, zaczynając od danego wierzchołka v, odkładamy indeks aktualnie rozpatrywanego wierzchołka na stosie, wybieramy dowolną krawędź z nim incydentną, przechodzimy po niej do kolejnego wierzchołka i usuwamy tę krawędź z grafu. Operację tę powtarzamy tak długo, dopóki nie znajdziemy się w wierzchołku, który nie ma już więcej krawędzi.
Zauważmy, że proces ten musi się zakończyć w wierzchołku v. Wynika to z faktu, że jeżeli stopnie wszystkich w wierzchołków w grafie były parzyste, wówczas jeżeli obecnie rozpatrywany wierzchołek jest różny od wierzchołka początkowego, to w grafie znajdują się dokładnie dwa wierzchołki nieparzystych stopni – początkowy oraz obecny. Skoro aktualnie rozpatrywany wierzchołek jest nieparzystego stopnia, możemy go opuścić, przechodząc do kolejnego. Stąd wynika, przez zaprzeczenie, że jeżeli wierzchołka nie możemy opuścić, to jest on wierzchołkiem początkowym.
Jedną z możliwości jest przejście całego cyklu Eulera w punktach 4 – 8 całego cyklu. Jeśli ono nastąpi, to kończy dowód, ponieważ późniejszy powrót do pętli WHILE w kroku 12 nic nie zmienia. W przeciwnym wypadku wszystkie pozostałe w grafie wierzchołki są parzystego stopnia (ponieważ usunęliśmy z każdego parzystą liczbę krawędzi), chociaż mogą nie być połączone. Wynika stąd, że każda spójna składowa grafu G’ pozostałego po usunięciu pewnego cyklu w krokach 4 – 8 posiada cykl Eulera. Zwróćmy uwagę na fakt, że usunięta właśnie ścieżka cykliczna łączy te trasy w cykl Eulera dla wejściowego grafu. Gdyby tak nie było, wówczas suma pozostałych spójnych składowych i usuniętego w krokach 4 – 8 cyklu nie byłaby grafem spójnym, co przeczy założeniu.
W krokach 9 – 12 opisanego algorytmu, zdejmując ze stosu kolejne wierzchołki przemierzamy (od końca, ale to nie zmienia dowodu) ścieżkę cykliczną, zbaczając z niej w każdym przypadku, gdy natrafimy na nieizolowany wierzchołek (gdy spełniony będzie warunek 4). Następnie przyjmujemy aktualnie zdjęty ze stosu wierzchołek za wierzchołek początkowy i powracając w do kroku 4 wywołujemy rekurencyjnie algorytm znajdujący trasę Eulera dla spójnej składowej. Zauważmy, że każda taka podtrasa jest właściwą trasą Eulera, która prowadzi z powrotem do wierzchołka na ścieżce cyklicznej, na której się rozpoczęła, co wynika zresztą z indukcyjnego założenia dowodu.
Należy dodatkowo zauważyć, że każda podtrasa może się zetknąć ze ścieżką cykliczną wiele razy. W takim przypadku jednak każdą podtrasę i tak przemierzymy tylko jeden raz – wtedy, kiedy na nią wejdziemy.
- Definicja Algorytm Floyda-Warshalla służy do znajdowania najkrótszych ścieżek pomiędzy wszystkimi parami wierzchołków w grafie ważonym.
- Opis algorytmu Algorytm Floyda-Warshalla korzysta z tego, że jeśli najkrótsza ścieżka pomiędzy wierzchołkami v1 i v2 prowadzi przez wierzchołek u, to jest ona połączeniem najkrótszych ścieżek pomiędzy wierzchołkami v1 i u oraz u i v2. Na początku działania algorytmu inicjowana jest tablica długości najkrótszych ścieżek, tak że dla każdej pary wierzchołków (v1,v2) ich odległość wynosi:
- Wydajność algorytmu - Złożoność obliczeniowa:
- Zapis w pseudokodzie Dla grafu G i funkcji wagowej w otrzymamy tablicę d[v1][v2] odległości pomiędzy wierzchołkami v1 i v2.
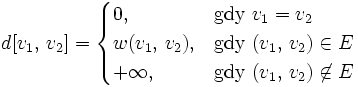
Algorytm jest dynamiczny i w kolejnych krokach włącza do swoich obliczeń ścieżki przechodzące przez kolejne wierzchołki. Tak więc w k-tym kroku algorytm zajmie się sprawdzaniem dla każdej pary wierzchołków, czy nie da się skrócić (lub utworzyć) ścieżki pomiędzy nimi przechodzącej przez wierzchołek numer k (kolejność wierzchołków jest obojętna, ważne tylko, żeby nie zmieniała się w trakcie działania programu). Po wykonaniu |V| takich kroków długości najkrótszych ścieżek są już wyliczone.
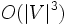
- Złożoność pamięciowa:
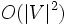
- Definicja Algorytm Johnsona - algorytm znajdowania najkrótszych ścieżek między wszystkimi parami wierzchołków. Działa w czasie O( | V |² lg | V | + | V | | E | ) (zakładając, że wykonuje algorytm Dijkstry przy użyciu kolejek priorytetowych opartych o kopce Fibonacciego), dla grafów rzadkich jest więc asymptotycznie szybszy od algorytmu Floyda-Warshalla. Algorytm Johnsona zwraca albo macierz wag najkrótszych ścieżek, albo informuje, że graf wejściowy ma cykl o ujemnej wadze. W algorytmie Johnsona jako podprogramy używane są algorytmy Dijkstry i Bellmana-Forda.
- Opis Istota algorytmu polega na zastosowaniu metody zmieniających się wag, jeśli wszystkie wagi krawędzi w grafie G=(V,E) są nieujemne, wtedy najkrótsze ścieżki między wszystkimi parami wierzchołków wyznaczane są za pomocą algorytmu Dijkstry, z każdego wierzchołka oddzielnie. Dla grafu o wagach ujemnych obliczyć trzeba nowy zbiór nieujemnych wag krawędzi, aby zastosować algorytm Dijkstry. Wyliczony nowy zbiór wag musi spełniać zależności:
- Zastosowanie - Sterowanie procesami dyskretnymi
- dla wszystkich par wierzchołków najkrótsza ścieżka z wierzchołka u do v dla funkcji wagowej jest także najkrótszą ścieżką pomiędzy tymi wierzchołkami, dla nowej funkcji wagowej,
- dla wszystkich krawędzi grafu G, nowa waga jest nieujemna.
- W planowaniu i kontroli produkcji
- Algorytmy usuwania lewostronnej rekursji
- Algorytm Johnsona dla procesów przepływowych 2 i 3 magazynowych
- Szeregowanie operacji dla linii produkcyjnej.
- Definicja Zrozumienie algorytmu wymaga znajomości pojęć grafu oraz minimalnego drzewa rozpinającego. Algorytm Kruskala wyznacza minimalne drzewo rozpinające dla grafu nieskierowanego ważonego, o ile jest on spójny. Innymi słowy, znajduje drzewo zawierające wszystkie wierzchołki grafu, którego waga jest najmniejsza możliwa. Jest to przykład algorytmu zachłannego.
- Algorytm 1. Utwórz las L z wierzchołków oryginalnego grafu – każdy wierzchołek jest na początku osobnym drzewem.
- Implementacja i złożoność Jako zbiór S można wziąć tablicę wszystkich krawędzi posortowaną według wag. Wtedy w każdym kroku najmniejsza krawędź to po prostu następna w kolejności. Sortowanie działa w czasie O(ElogE) = O(ElogV) (ponieważ E < V², zatem logE < 2logV).
- Przykład Dany jest spójny graf nieskierowany:
Został on po raz pierwszy opublikowany przez Josepha Kruskala w 1956 roku.
2. Utwórz zbiór S zawierający wszystkie krawędzie oryginalnego grafu.
3. Dopóki S nie jest pusty:
- Wybierz i usuń z S krawędź o minimalnej wadze.
- Jeśli krawędź ta łączyła dwa różne drzewa, to dodaj ją do lasu L, tak aby połączyła dwa odpowiadające drzewa w jedno.
- W przeciwnym wypadku odrzuć ją.
Po zakończeniu algorytmu L jest minimalnym drzewem rozpinającym.
Drugą fazę algorytmu można zrealizować przy pomocy struktury zbiorów rozłącznych – na początku każdy wierzchołek tworzy osobny zbiór, struktura pozwala na sprawdzenie, czy dwa wierzchołki są w jednym zbiorze i ewentualne połączenie dwu zbiorów w jeden. Przy implementacji przez tzw. las drzew rozłącznych z kompresją ścieżki operacje te łącznie działają w czasie O(Eα(E,V)), gdzie α jest niezwykle wolno rosnącą funkcją (odwrotnością funkcji Ackermanna).
Całkowity czas działania jest zatem O(ElogV), ze względu na pierwszą fazę – sortowanie. Jeśli wagi krawędzi są już na wejściu posortowane, albo pozwalają na użycie szybszych algorytmów sortowania (na przykład sortowania przez zliczanie), algorytm działa w czasie O(Eα(E,V)).
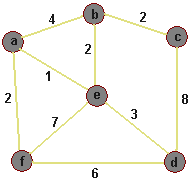
Po posortowaniu krawędzi wg. wag otrzymamy:
1. Krawędź ae=1
2. Krawędź af=2
3. Krawędź bc=2
4. Krawędź be=2
5. Krawędź de=3
6. Krawędź ab=4
7. Krawędź fd=6
8. Krawędź ef=7
9. Krawędź cd=8
Wszystkie wierzchołki należą do jednego drzewa- minimalnego drzewa rozpinającego. Suma wag krawędzi wchodzących w skład drzewa wynosi 10.
- Definicja Algorytm Prima lub algorytm Dijkstry-Prima – algorytm zachłanny wyznaczający tzw. minimalne drzewo rozpinające (MDR). Mając do dyspozycji graf nieskierowany i spójny, tzn. taki w którym krawędzie grafu nie mają ustalonego kierunku oraz dla każdych dwóch wierzchołków grafu istnieje droga pomiędzy nimi, algorytm oblicza podzbiór E' zbioru krawędzi E, dla którego graf nadal pozostaje spójny, ale suma kosztów wszystkich krawędzi zbioru E' ma najmniejszą możliwą wartość.
- Algorytm Algorytm Prima wygląda tak:
- Dowód poprawności Niech dany będzie graf G = <V, E> oraz dwa algorytmy: algorytm Prima, oraz niezachłanny i poprawny algorytm znajdowania MDR. Załóżmy, że drzewo spinające znalezione przez algorytm Prima nie jest minimalne.
- Przykład Przyjmijmy następującą notację: [ui, uj, w] oznacza krawędź łączącą wierzchołki (ui, uj) o wadze w.
Grafy zawierające dużo krawędzi, w których dwa te same wierzchołki połączone są np. trzema krawędziami lub pomiędzy dwoma wierzchołkami istnieje np. 5 różnych dróg długości 2, raczej nie są "lubiane" przez algorytmy i często przekształcenie takiego skomplikowanego grafu w graf mu równoważny pod względem zachowania możliwych połączeń przynosi znaczące korzyści.
1. Utwórz drzewo zawierające jeden wierzchołek, dowolnie wybrany z grafu.
2. Powtarzaj kolejno dla wszystkich dodawanych do drzewa wierzchołków:
- utwórz zbiór zawierający wszystkie krawędzie tego wierzchołka,
- usuń ze zbioru krawędź o najmniejszej wadze, łączącą wierzchołek z drzewa z wierzchołkiem spoza drzewa,
- dodaj tę krawędź i wierzchołek do drzewa.
Złożoność obliczeniowa (m to liczba krawędzi a n to liczba wierzchołków):
- przy użyciu macierzy sąsiedztwa oraz tablicy: O(n²)
- przy użyciu kopca binarnego: O(m log(n))
- przy użyciu kopca Fibonacciego O(m + n log(n)), co przy dużej gęstości grafu (takiej, że m jest ω(n log (n)) oznacza duże przyśpieszenie
Zakładamy, że drugi algorytm, podobnie jak algorytm Prima pobiera kolejne gałęzie grafu wejściowego, dołączając je do początkowo pustego drzewa wynikowego (odpowiednio Tp i Topt). Załóżmy, że dla pierwszych i gałęzi algorytmy zadziałały tak samo, tj.
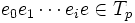
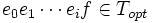
krawędzie f i e są różne.
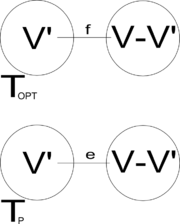Niech V' oznacza zbiór wierzchołków grafu G połączonych krawędziami 
.
Ponieważ wybór e był niezachłanny, to waga e jest nie większa niż waga f.
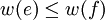
Niech
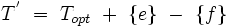
Wtedy T' jest drzewem, ponieważ Topt jest drzewem, a krawędzie e i f mają tę własność, iż jeden z ich końców należy do Topt, a drugi prowadzi na jego zewnątrz.
A ponieważ
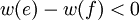, to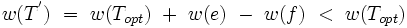
co jest sprzeczne z wyborem Topt.
Podobne rozumowanie można przeprowadzić dla kolejnych dołączanych do drzew wynikowych krawędzi.
Wniosek – nie może istnieć drzewo spinające o sumie wag mniejszej, niż drzewo odnalezione algorytmem Prima – algorytm Prima zawsze odnajduje minimalne drzewo spinające.
Przebieg algorytmu:
Suma wag krawędzi wchodzących w skład drzewa wynosi 10.
- Opis Przeszukiwanie grafu lub inaczej przechodzenie grafu to czynność polegająca na odwiedzeniu w jakiś usystematyzowany sposób wszystkich wierzchołków grafu w celu zebrania potrzebnych informacji. Często podczas przejścia grafu rozwiązujemy już jakiś problem, ale przeważnie jest to tylko wstęp do wykonania właściwego algorytmu.
- Przeszukiwanie wszerz (BFS) 1. Definicja
- Przeszukiwanie w głąb (DFS) 1. Definicja
Powszechnie stosuje się dwie podstawowe metody przeszukiwania grafów:
- przeszukiwanie wszerz (BFS)
- przeszukiwanie w głąb (DFS)
Odrębnym zagadnieniem jest przechodzenie drzew, zwłaszcza binarnych które jest niewątpliwie przeszukiwaniem grafu. Wyróżnia się trzy metody przechodzenia drzew, przy czym ostatnia metoda dotyczy tylko drzew binarnych:
- pre-order
- post-order
- in-order
Przeszukiwanie wszerz (ang. Breadth-first search, w skrócie BFS) – w informatyce algorytm przeszukiwania grafu używany do przechodzenia lub przeszukiwania drzewa lub grafu. Algorytm zaczyna od korzenia i odwiedza wszystkie połączone z nim węzły. Następnie odwiedza węzły połączone z tymi węzłami i tak dalej, aż do odnalezienia celu.
2. Algorytm
Pseudokod:
Animowany przykład algorytmu przeszukiwania wszerz:
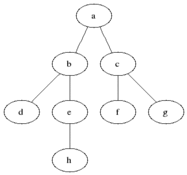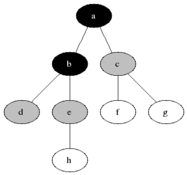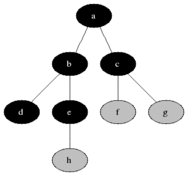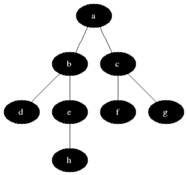
3. Właściwości
a) Złożoność pamięciowa- Ponieważ trzeba utrzymywać listę węzłów które się już odwiedziło, złożoność pamięciowa przeszukiwania wszerz wynosi O(|V| + |E|), gdzie |V| to liczba węzłów, a |E| to liczba krawędzi w grafie. Z powodu tak dużego zapotrzebowania na pamięć przeszukiwanie wszerz jest niepraktyczne dla dużych danych.
b)Złożoność czasowa- Ponieważ w najgorszym przypadku przeszukiwanie wszerz musi przebyć wszystkie krawędzie prowadzące do wszystkich węzłów, złożoność czasowa przeszukiwania wszerz wynosi O(|V| + |E|), gdzie |V| to liczba węzłów, a |E| to liczba krawędzi w grafie.
c) Kompletność- Przeszukiwanie wszerz jest kompletne, to znaczy że gdy istnieje rozwiązanie, przeszukiwanie wszerz odnajdzie je niezależnie od grafu.
4. Zastosowania
Przeszukiwanie wszerz może zostać użyte do rozwiązania wielu problemów z teorii grafów, dla przykładu:
- Odnalezienie wszystkich połączonych węzłów w grafie
- Odnalezienie najkrótszej ścieżki między dwoma wierzchołkami (nie uwzględnia wag krawędzi w grafie ważonym)
- sprawdzania czy graf jest dwudzielny
Przeszukiwanie w głąb (ang. Depth-first search, w skrócie DFS) – w informatyce algorytm przeszukiwania grafu używany do przechodzenia lub przeszukiwania drzewa lub grafu. Przeszukiwanie zaczyna się od korzenia i porusza się w dół do samego końca gałęzi, po czym wraca się o jeden poziom i próbuje kolejne gałęzie itd.
2. Przykład
Przyjrzyjmy się poniższemu grafowi:
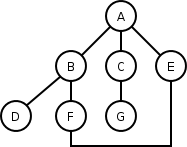
Zakładając że najpierw wybiera się węzły z lewej strony, później te z prawej, przeszukiwanie zaczynając od A, odwiedzi się węzły w tej kolejności (w nawiasach oznaczone powroty):
A, B, D, (B), F, E, (F), (B), (A), C, G, (C), (A).
3. Właściwości
a) Złożoność pamięciowa- Złożoność pamięciowa przeszukiwania w głąb w przypadku drzewa jest o wiele mniejsza niż przeszukiwania wszerz, gdyż algorytm w każdym momencie wymaga zapamiętania tylko ścieżki od korzenia do bieżącego węzła, podczas gdy przeszukiwanie wszerz wymaga zapamiętywania wszystkich węzłów w danej odległości od korzenia, co zwykle rośnie wykładniczo w funkcji długości ścieżki.
b) Złożoność czasowa- Złożoność czasowa obu algorytmów jest proporcjonalna do sumy liczby wierzchołków i liczby krawędzi w przeszukiwanym grafie.
c) Zupełność (kompletność)- Algorytm jest zupełny (czyli znajduje rozwiązanie lub informuje, że ono nie istnieje) dla drzew skończonych. Grafy skończone wymagają oznaczania już odwiedzonych wierzchołków. Dla grafów nieskończonych nie jest zupełny.
4. Zastosowania
Przeszukiwanie w głąb jest często stosowanym algorytmem w teorii grafów. Używa się go m.in. do:
- Znajdywania najkrótszych ścieżek między dwoma wierzchołkami w drzewie.
- Sprawdzania, czy istnieje ścieżka między dwoma wierzchołkami w grafie.
- Wyznaczania spójnych składowych.
Rozwiązania poniższych problemów teoriografowych opierają się na przeszukiwaniu w głąb:
- Wyznaczanie silnie spójnych składowych w grafie skierowanym.
- Sortowanie topologiczne skierowanego grafu acyklicznego.
Ponadto algorytm ten jest często spotykany w rozwiązaniach typu brute force problemów z innych dziedzin. Bazuje na nim zdecydowana większość algorytmów służących do przeglądania drzewa gry, np. min-max, czy też alpha-beta.
- Definicja Algorytm najbliższego sąsiada - naiwny algorytm rozwiązywania problemu komiwojażera polegający na odwiedzaniu, począwszy od wybranego wierzchołka, wierzchołka znajdującego się najbliżej wierzchołka ostatnio odwiedzonego. Bardzo prosty do zaprogramowania, szybki, ale daje słabe wyniki.
- Opis Większość algorytmów grupowania została opracowana właśnie w oparciu o zbiory klasyczne. Najbardziej znanymi i rozpowszechnionymi wśród nich są algorytmy: najbliższego sąsiada, k najbliższych sąsiadów, MMD, drzewa minimalnego.
Schemat postępowania algorytmu najbliższego sąsiada można zapisać następująco:
1. Obliczenie odległości elementów od ich najbliższych sąsiadów
2. Określenie sposobu obliczania wartości progowej
3. Połączenie w grupę każdej pary elementów, której odległość jest mniejsza od ustalonej wartości progowej
Algorytm k najbliższych sąsiadów różni się od algorytmu najbliższego sąsiada tym, że do grupy dołączamy nie tylko najbliższego sąsiada rozpatrywanego elementu, lecz k sąsiadów. Zaletą tego algorytmu w porównaniu z algorytmem najbliższego sąsiada są dobre wyniki uzyskiwane dla grup o nierównomiernym rozkładzie gęstości.