Pojęcia służące do opisu grafów
Lista definicji (alfabetycznie)
- Acentryczność wierzchołka grafu To maksymalna odległości wierzchołka do innych wierzchołków grafu, lub inaczej długość najdłuższej ścieżki prostej zaczynającej się w danym wierzchołku.
- Cykl Zamknięta droga prosta
- Droga Wyznaczona przez krawędzie trasa polegająca na podróżowaniu od wierzchołka do wierzchołka po łączących je krawędziach. Jeżeli przez e(i) oznaczy się i-tą krawędź grafu, to droga może być jednoznacznie zapisana jako
- Droga prosta Droga nie zawierająca dwóch tych samych krawędzi
- Długość drogi/ścieżki To liczba krawędzi/wierzchołków tworzących daną drogę/ścieżkę
- Droga acykliczna Droga nie zawierająca cyklu
- Gęstość grafu Stosunek liczby krawędzi do największej możliwej liczby krawędzi:
- Klika Podzbiór wierzchołków danego grafu, z których każdy jest sąsiadem każdego innego (czyli podgraf pełny).
- Kolorowanie grafu To nadanie każdemu wierzchołkowi koloru, tak by żadne sąsiadujące ze sobą wierzchołki nie były pokolorowane tym samym kolorem.
- Krawędzie sąsiednie Krawędzie kończące się w jednym wierzchołku. W przypadku grafów skierowanych zazwyczaj wymagana jest "zgodność kierunków" krawędzi, tj. dwie krawędzie są sąsiednie, jeżeli odpowiednio kończą się i zaczynają w tym samym wierzchołku.
- Krawędź/wierzchołek krytyczny Krawędź/wierzchołek, po usunięciu której/którego ze zbioru pokrywającego zmniejsza się indeks pokrycia krawędziowego/wierzchołkowego.
- Liczba chromatyczna Najmniejsza liczba kolorów potrzebna do prawidłowego pokolorowania grafu.
- Nadgraf grafu H Taki graf, że H jest jego podgrafem.
- Pętla Krawędź zaczynająca i kończąca się w tym samym wierzchołku
- Podgraf grafu H Graf G uzyskany poprzez usunięcie części wierzchołków z H, wraz z kończącymi się w nich krawędziami
- R-regularny graf Graf, w którym każdy wierzchołek grafu jest stopnia r.
- Sąsiad: Dwa wierzchołki są sąsiadami, jeśli istnieje krawędź pomiędzy nimi.
- Spójna składowa grafu G Spójna składowa grafu to możliwie największy spójny podgraf grafu G. Graf spójny ma jedną spójną składową.
- Stopień wierzchołka v Liczba kończących się w nim krawędzi. Oznaczenie: deg(v). W przypadku grafów skierowanych mówi się o stopniach wejściowym i wyjściowym – degIn(v), degOut(v)
- Ściana Obszar zamknięty wyznaczony przez krawędzie grafu (tzw. krawędzie tworzące ścianę). Z pojęciem ściany ściśle powiązane jest twierdzenie Eulera. Uwaga! Za ścianę uważa się też nieskończony obszar znajdujący się "na zewnątrz" grafu (a więc każdy graf ma co najmniej jedną ścianę)!
- Ściany sąsiadujące Ściany są sąsiadujące, jeżeli mają co najmniej jedną wspólną krawędź tworzącą.
- Ścieżka Intuicyjnie jest bardzo podobna do drogi, z tym, że jest wyznaczona przez wierzchołki, tj. można ją opisać poprzez ciąg wierzchołków
- Ścieżka prosta Ścieżka wyznaczona tak, by żaden wierzchołek na trasie nie powtarzał się
- Ścieżka zamknięta Ścieżka
- Usunięcie wierzchołka Przez usunięcie wierzchołka rozumie się wymazanie go, oraz wszystkich kończących się w nim krawędzi z danego grafu
- Waga krawędzi Często od grafu reprezentującego np. sieć połączeń komunikacyjnych oczekuje się nie tylko informacji o istniejącym połączeniu (krawędzi lub ścieżki), ale też o np. długości połączenia. Wprowadza się wtedy wagi, wartość przypisaną każdej krawędzi. Graf taki można wykorzystać np. do wyznaczenie optymalnej, w sensie przejechanych kilometrów trasy, lub, ogólniej rozwiązanie problemu komiwojażera, wyznaczenia optymalnego rozłożenia kabli w sieci, koordynowania wysyłania plików metodą peer to peer itp.
- Wierzchołek izolowany Wierzchołek o stopniu 0, czyli nie będący końcem żadnej krawędzi.
- Wierzchołek pokrywający krawędź Wierzchołek v pokrywa krawędź e, jeżeli e kończy się w v. W analogiczny sposób definiuje się krawędź pokrywającą dany wierzchołek – krawędź e kryje wierzchołek v, gdy się w nim kończy.
- Wierzchołek rozpajający Wierzchołek, po usunięciu którego zwiększa się liczba spójnych składowych grafu. Nazywany przegubem tworzy "wąskie gardło" grafu – tj. istnieją w grafie dwa wierzchołki takie, że każda łącząca je droga musi przejść przez wierzchołek rozpajający.
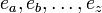 , taka, że krawędź e(z) kończy się w początkowym wierzchołku drogi
, taka, że krawędź e(z) kończy się w początkowym wierzchołku drogiNa tym rysunku nie ma cykli, czyli wszystkie drogi są proste (patrz def. niżej)
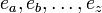
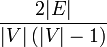 .
.Używa się również określeń: graf gęsty, jeżeli ma on dużo krawędzi w stosunku do liczby wierzchołków i podobnie graf rzadki, jeżeli ma on mało krawędzi w stosunku do liczby wierzchołków. Przy czym znaczenie słów mało i dużo może zależeć od kontekstu.
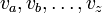
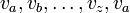 , czyli kończąca się w początkowym wierzchołku
, czyli kończąca się w początkowym wierzchołku
- Minimalny pokrywający podzbiór krawędzi/wierzchołków
To możliwie najmniejszy podzbiór krawędzi/wierzchołków grafu, taki, że pokrywają one wszystkie wierzchołki/krawędzie danego grafu. Liczność minimalnego zbioru pokrywającego krawędzi/wierzchołków nazywa się indeksem pokrycia wierzchołkowego/krawędziowego. Wszystkie podzbiory o tej liczności i własności nazywa się pokryciem minimalnym.
- Most
Krawędziowy "odpowiednik" wierzchołka rozpajającego – krawędź, po usunięciu której wzrasta liczba spójnych składowych grafu.
Oznaczenia formalne
Często dla danego grafu G stosuje się skrócone oznaczenia oparte na alfabecie greckim oraz łacińskim:
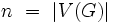 liczba wierzchołków G
liczba wierzchołków G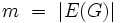 liczba krawędzi G
liczba krawędzi G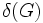 najmniejszy stopień wierzchołka w G
najmniejszy stopień wierzchołka w G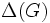 największy stopień wierzchołka w G
największy stopień wierzchołka w G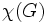 liczba chromatyczna G
liczba chromatyczna G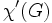 indeks chromatyczny G
indeks chromatyczny G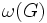 liczba spójnych składowych G
liczba spójnych składowych G
Przyklad
To przykład grafu nieskierowanego G wraz z jego ilustracją:
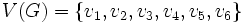
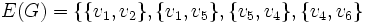 ,
,
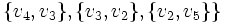
Jego własności:
- Przykładową ścieżką prostą może być
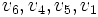 a cyklem
a cyklem 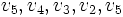
- Stopnie wierzchołków:
- Krawędź
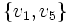 jest sąsiednia z
jest sąsiednia z 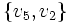 , ale nie jest z
, ale nie jest z 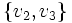
- Graf G ma trzy ściany – zewnętrzną oraz dwie wyznaczone odpowiednio przez ścieżki np.
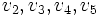 i
i 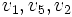
- Graf G jest spójny, czyli ma jedną spójną składową. Natomiast podgraf grafu G, składający się z wierzchołków
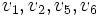 i incydentnych z nimi krawędziami, ma dwie spójne składowe – cykl
i incydentnych z nimi krawędziami, ma dwie spójne składowe – cykl
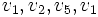 i wierzchołek izolowany v6.
i wierzchołek izolowany v6.
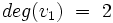 ,
,
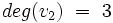 ,
,
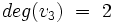 ,
,
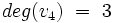 ,
,
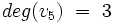 ,
,
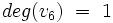
Izomorfizm i homeomorfizm grafów
- Izomorfizm grafów Graficzna reprezentacja grafów (w postaci kropek i łączących je krzywych) jest tylko sposobem przedstawienia relacji zachodzącej między wierzchołkami. Dla każdego grafu istnieje nieskończenie wiele przedstawiających go jednoznacznie wykresów, rysunków. Co więcej, właściwości grafów (takie jak większość podanych w następnej sekcji) są niezależne od sposobu numerowania wierzchołków, kolejności ich rysowania itp. Grafy różniące się tylko sposobem ich przedstawienia, lub indeksami nadanymi wierzchołkom, nazywamy izomorficznymi.
- Homeomorfizm grafów Dwa grafy są homeomorficzne, jeśli z jednego grafu można otrzymać drugi zastępując wybrane krawędzie łańcuchami prostymi lub łańcuchy proste pojedynczymi krawędziami. Mówiąc obrazowo, chodzi o dorysowywanie na krawędziach dowolnej liczby wierzchołków, bądź wymazywanie ich.
Klasy grafów
Grafy można podzielić ze względu na różne własności, zazwyczaj zachowane w obrębie izomorfizmów danego grafu. Najczęściej dotyczą one tylko grafów prostych (nie zawierających pętli i krawędzi wielokrotnych), część z tych własności można rozszerzyć na multigrafy. Najczęściej spotykane klasy grafów to:
- Graf prosty (właściwy) Graf nie zawierający pętli ani krawędzi wielokrotnych. Graf nieprosty nazywany jest mulitigrafem. Z reguły zdanie G jest grafem oznacza w domyśle, że G jest grafem prostym
- Graf pełny Graf, którego każdy wierzchołek jest połączony bezpośrednio krawędzią z każdym innym. Graf pełny o n wierzchołkach oznacza się
- Graf regularny stopnia k Graf, którego każdy wierzchołek jest stopnia k
- Graf kubiczny Specjalne określenie dla grafów regularnych stopnia 3
- Graf acykliczny Graf nie zawierający żadnej drogi zamkniętej
- Graf spójny Graf, w którym dla każdego wierzchołka istnieje droga do każdego innego wierzchołka
- Graf k-spójny Graf posiadający k spójnych składowych
- Drzewo Spójny graf acykliczny
- Las Graf, którego wszystkie spójne składowe są drzewami
- Graf dwudzielny Graf, którego wierzchołki mogą być podzielone na dwa zbiory, tak by w obrębie jednego zbioru żaden wierzchołek nie był połączony z innym
- Graf dwudzielny pełny Graf dwudzielny taki, że każdy wierzchołek z jednego zbioru jest połączony krawędzią z każdym wierzchołkam ze zbioru drugiego. Pełny graf dwudzielny o
- Graf k-dzielny To naturalne rozszerzenie klasy grafów dwudzielnych – jest to graf, którego zbiór wierzchołków można podzielić na k parami rozłącznych podzbiorów takich, że żadne dwa węzły należące do tego samego zbioru nie są połączone krawędzią
- Pełny graf k-dzielny Jeżeli zbiór wierzchołków dzieli się na k nie połączonych między sobą podzbiorów wierzchołków, to jeżeli dla każdego wierzchołka
- Graf eulerowski Graf posiadający drogę prostą przechodzą przez każdą krawędź.
- Graf hamiltonowski Graf posiadający ścieżkę prostą przechodzą przez każdy wierzchołek.
- Graf planarny Graf, dla którego istnieje graf izomorficzny, który można przedstawić na płaszczyźnie tak, by żadne krawędzie się nie przecinały (oczywiście, nie w sensie "spotkania się" w jednym wierzchołku). Kazimierz Kuratowski udowodnił, że grafy pełne K5 i K3,3 są nieplanarne, oraz że każdy inny graf nieplanarny musi posiadać podgraf homeomorficzny z którymś z tych grafów.
- Graf płaski To izomorficzne przedstawienie grafu takie, że żadne dwie krawędzie się nie przecinają
- Graf platoński Graf, którego przedstawienie tworzy siatkę wielościanu foremnego
- Graf komórkowy Graf płaski, którego wszystkie ściany są utworzone przez drogi zamknięte tej samej długości
- Graf krytyczny Graf, którego każdy wierzchołek/krawędź jest krytyczny/krytyczna
- Graf symetryczny Graf skierowany taki, że jeżeli istnieje krawędź (u, v) to istnieje też krawędź (v, u). Graf asymetryczny ma własność: jeżeli istnieje krawędź (u, v) to nie istnieje krawędź (v, u).
- Graf podstawowy grafu skierowanego To niemal ten sam, ale nieskierowany, bo bez zwrotów na krawędziach
- Turniej To graf pełny, w którym zorientowano krawędzie, lub inaczej, graf skierowany którego graf podstawowy jest grafem pełnym
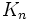 .
.
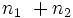 wierzchołkach oznacza się
wierzchołkach oznacza się
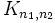
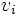 z j-tego przedziału
z j-tego przedziału 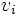 jest połączony z każdym wierzchołkiem z każdego z przedziałów poza j, to jest to pełny graf k-dzielny
jest połączony z każdym wierzchołkiem z każdego z przedziałów poza j, to jest to pełny graf k-dzielny