Poprzednia Następna

Definicja
Permutacja – wzajemnie jednoznaczne przekształcenie pewnego zbioru na siebie. Najczęściej termin ten jest używany w odniesieniu do permutacji zbiorów skończonych. Permutacje zbiorów skończonych mogą być utożsamiane z ustawianiem elementów zbioru w pewnej kolejności. W poniższym artykule zbiór wszystkich permutacji zbioru X będzie oznaczany S(X), jeżeli X={1, 2, 3, ..., n}, to zapisywany on będzie symbolem S_n (zob. pozostałe oznaczenia w artykule o grupach permutacji).

Zapis
W celu skrócenia zapisu, szczególnie, gdy permutacji nie można zadać prostym wzorem, permutację π∈S_n zapisuje się jako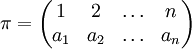
, gdy π(i) = a_i dla i=1,...,n, czyli permutacja π przypisuje liczbie i wartość a_i.

Zapis macierzowy
Permutację można też zapisać jako macierz A, taką, że
.
Na przykład permutację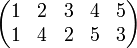

można zapisać jako


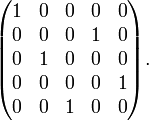
Grupa permutacji
Definicja
Grupa permutacji – grupa wszystkich bijekcji pewnego zbioru w siebie (czyli permutacji) z działaniem składania pełniącego rolę działania grupowego i identycznością jako elementem neutralnym. Elementem odwrotnym do danego jest funkcja (permutacja) odwrotna do danej, która zawsze istnieje z definicji bijekcji.
Niekiedy nazywana jest ona także grupą symetryczną, zaś przez niektórych autorów nazwa grupy permutacji stosowana jest na określenie jej (właściwej) podgrupy.

Zbiór S(X) wszystkich permutacji zbioru X wraz z działaniem składania funkcji stanowi grupę nazywaną grupą permutacji. Jeśli X jest zbiorem n-elementowym, to grupa S(X) jest izomorficzna z S_n:
niech f:{1,...,n}→X będzie bijekcją. Wówczas odwzorowanie
S(X)→S_n; π→f^(-1) ο π ο f
jest izomorfizmem grup.
Podobnie można pokazać, że jeśli zbiory X,Y są równoliczne, to grupy S(X),S(Y) są izomorficzne, a więc nierozróżnialne na gruncie teorii grup.
Rząd grupy S_n, czyli moc zbioru wszystkich permutacji zbioru n-elementowego, to możliwa liczba uporządkowań tego zbioru równa n!, gdzie wykrzyknik oznacza silnię. W kombinatoryce na oznaczenie liczności tego zbioru stosuje się również symbol P_n.

Składanie permutacji
Złożeniem permutacji π₁π₂∈S(X) jest permutacja π₂ ο π₁∈S(X) zadana wzorem
(π₂ ο π₁)(x)=π₂(π₁(x)) dla x∈X.
Przykład
.

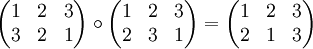Permutacja odwrotna
Permutacja odwrotna π^(-1) do permutacji π∈S_n, która odwzorowuje w zapisie macierzowym wiersz górny na dolny, to permutacja odwzorowująca dolny wiersz na górny: aby uzyskać macierz w zapisie macierzowym należy zamienić porządek wierszy i (dla wygody) uporządkować rosnąco kolumny.
Przykład
Jeśli 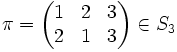, to
.

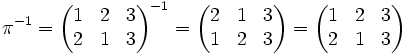Znak permutacji
Definiujemy go jako znak wyznacznika macierzy tej permutacji. Można na to spojrzeć też w inny sposób: każdą permutację można otrzymać za pomocą złożenia różnych ilości przestawień (transpozycji) par elementów. Takie przedstawienie permutacji nie jest jednoznaczne i można zmienić ilość użytych transpozycji, niemniej jednak liczba transpozycji w takiej reprezentacji jest zawsze albo parzysta albo nieparzysta. Inaczej mówiąc, parzystość liczby transpozycji jest niezmiennikiem tej operacji. Wynika to z faktu, że każda transpozycja zmienia całkowitą liczbę inwersji o liczbę nieparzystą. Permutację, która ma parzystą liczbę inwersji nazywamy parzystą (lub dodatnią), zaś jeśli ma ona nieparzystą liczbę inwersji to nazywamy ją permutacją nieparzystą (lub ujemną).

Cykle
Cyklem nazywamy każdą permutację postaci:
.
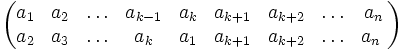Zazwyczaj, gdy operujemy na cyklach opuszczamy część: 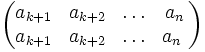, gdyż nie wnosi ona nic nowego.

Zapis cyklu możemy jeszcze uprościć. Wystarczy zauważyć że dolny wiersz naszego symbolu oznaczającego cykl można jednoznacznie odtworzyć z górnego. Zatem nasz ostateczny uproszczony symbol przybiera postać:

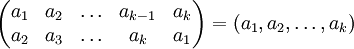
Można udowodnić (choć jest to dość intuicyjne), że każdą permutację można przedstawić jako złożenie pewnej liczby cykli.
Składanie permutacji podobnie jak większości funkcji nie jest przemienne. Nie dotyczy to sytuacji, gdy składamy permutacje niezależne. Ponieważ permutacjami niezależnymi są rozłączne cykle to zachodzi następujące twierdzenie:
πⁿ=p₁ⁿ ο p₂ⁿ ο ... p_kⁿ , gdzie π=p₁ ο p₂ ο p_k jest rozkładem permutacji π na k rozłącznych cykli.

Przykłady
Cyklem jest permutacja:
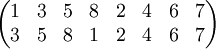, którą można zapisać jako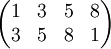
Rozkład na cykle


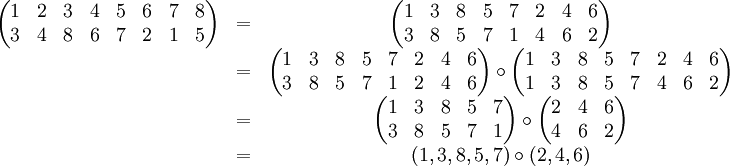
Kombinatoryka
Permutacja bez powtórzeń

Permutacja jest szczególnym przypadkiem wariacji bez powtórzeń.

Definicja: Permutacją bez powtórzeń zbioru złożonego z n różnych elementów nazywamy każdy n wyrazowy ciąg utworzony ze wszystkich wyrazów zbioru. Wszystkich możliwych permutacji zbioru n-elementowego jest:
P_n = n!

Przykład: Elementy zbioru A = {a,b,c} można ustawić w ciąg na P₃ = 3! = 6 sposobów: abc,acb,bac,bca,cab,cba.

Wyjaśnienie: W każdej z permutacji mamy do zapełnienia trzy wolne miejsca. W pierwszym z nich możemy umieścić dowolną z liter na trzy sposoby (P_n = 3 ⋅ ...), na drugim dowolną spośród pozostałych jeszcze dwóch liter na dwa sposoby (P_n = 3 ⋅ 2 ⋅ ...), itd. Na ostatnim miejscu musi znaleźć się ostatnia dostępna litera (element zbioru), a zatem możemy to zrobić tylko na jeden sposób. Ostatecznie otrzymujemy:
P_n = 3 ⋅ 2 ⋅ 1 = 3!

Permutacja z powtórzeniami

Niech A oznacza zbiór złożony z k różnych elementów A = {a₁,a₂,...,a_k}. Permutacją n elementową z powtórzeniami, w której elementy a₁,a₂,...,a_k powtarzają się odpowiednio n₁,n₂,...,n_k razy, n₁ + n₂ + ... + n_k = n, jest każdy n-wyrazowy ciąg, w którym elementy a₁,a₂,...,a_k powtarzają się podaną liczbę razy.
Liczba takich permutacji z powtórzeniami wynosi .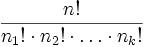

Przykład: Przestawiając litery b,a,b,k,a można otrzymać 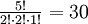różnych napisów.

Wyjaśnienie: "Zwykłe" przestawianie liter w słowie babka spowoduje kilkukrotne powstanie identycznych wyrazów, np. zamieniając miejscami pierwszą i trzecią literę znów otrzymamy słowo babka. Należy to uwzględnić przy zliczaniu, dlatego rezultat trzeba podzielić każdorazowo przez liczbę "zbędnych" permutacji, które nie prowadzą do powstania nowych słów (ciągów uporządkowanych).

Spostrzeżenie: Można wobec tego zapisać wzór na permutację bez powtórzeń następująco:
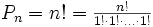(każdy z elementów występuje dokładnie raz).
Poprzednia Następna