Poprzednia Następna

Kombinacje bez powtórzeń
Definicja
Kombinacja bez powtórzeń to każdy podzbiór zbioru skończonego. Kombinacją k-elementową zbioru n-elementowego A nazywa się każdy k-elementowy podzbiór zbioru A (0≤k≤n). Używa się też terminu "kombinacja z n elementów po k elementów" lub wręcz "kombinacja z n po k".
Dopełnieniem kombinacji z n po k jest kombinacja z n po n-k. Liczba kombinacji z n po k wyraża się wzorem:

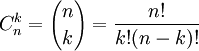
Przykłady

• Liczba kombinacji 2-elementowych zbioru 4-elementowego A={a, b, c, d} jest równa 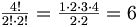. Kombinacjami są podzbiory: {a, b}, {a, c}, {a, d}, {b, c}, {b, d}, {c, d}.
• Prawdopodobieństwo trafienia "szóstki", tj. wszystkich liczb podczas losowania Lotto (wszystkich 6 z 49) wynosi
  
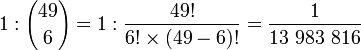
• Prawdopodobieństwo, że podczas losowania Lotto trafimy dokładnie k liczb spośród 6 (na 49) wynosi
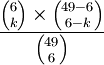
  Bierze się to stąd, że wszystkich możliwych wyników losowań jest ;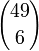
  na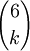 sposobów można trafić dokładnie k liczb spośród 6;
  na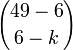 sposobów można chybić pozostałe 6-k liczb.
• Zatem prawdopodobieństwo trafienia "piątki" wynosi
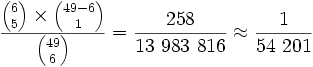
• "czwórki":
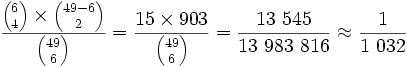
• "trójki":
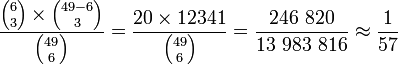
• Prawdopodobieństwo trafienia co najmniej trzech liczb można obliczyć jako
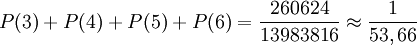  , gdzie P(x) to prawdopodobieństwo trafienia dokładnie x liczb.

Kombinacje z powtórzeniami
Definicja
Kombinacja z powtórzeniami (pojęcie matematyczne), to każdy multizbiór którego elementami są elementy pewnego zbioru skończonego. k-elementową kombinacją z powtórzeniami zbioru n-elementowego A nazywa się każdy k-elementowy multizbiór składający się z elementów zbioru A. W odróżnieniu do kombinacji bez powtórzeń tu elementy mogą się powtarzać.
Liczba k-elementowych kombinacji z powtórzeniami zbioru n-elementowego wyraża się wzorem:

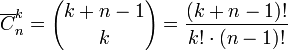
Pochodzenie wzoru
Jeżeli rozważymy zbiór {1,2,...,n}, to każdą jego k-elementową kombinacje da się uporządkować tak, by jej elementy a₁,a₂,...,a_k spełniały zależność:
1≤a₁≤a₂≤...≤a_k-1≤a_k≤n
co w liczbach naturalnych (wraz z zerem) równoważne jest kolejno
0<a₁<a₂+1<...<a_k-1+k-2<a_k+k-1<n+k
oraz, po zamianie współczynników
0<b₁<b₂<...<b_k-1<b_k<n+k
Ilość rozwiązań w takiego równania dla b1,b2,...,bk∈N jest równa ilości k-elementowych kombinacji bez powtórzeń zbioru (n + k - 1)-elementowego, czyli .
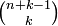Przyklady

• Liczba kombinacji 2-elementowych z powtórzeniami zbioru 4-elementowego A = {a, b, c, d} jest równa 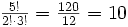. Można je wymienić: {a, b}, {a, c}, {a, d}, {b, c}, {b, d}, {c, d}, {a,a}, {b,b}, {c,c}, {d,d}. Kolejność nie ma tutaj znaczenia, równie dobrze można napisać {c,d}, jak {d,c}.
• Rozważmy rozmieszczenie k nierozróżnialnych elementów (np. kulek) w n komórkach (szufladkach) w taki sposób, że w każdej komórce może być kilka elementów.
  Przykładowo, dla n = 5 i k = 3:
  
  Zatem mamy rózne ułożenia 4 (n - 1) wewnętrznych kresek i 3 (k) kółek. Stąd

DODATKOWO:
Definicje obu kombinacji i program obliczający je on-line, znaleźć można na stronie math.edu.pl.

Poprzednia Następna