Poprzednia Następna

Liczby Bella
Definicja
Niech B_n będzie równe liczbie wszystkich partycji zbioru n-elementowego. (Przypomnijmy, że partycją zbioru nazywamy rodzine jego niepustych, parami rozłącznych podzbiorów, które w sumie dają cały zbiór). Korzystając z interpretacji kombinatorycznej liczb Stirlinga II rodzaju mamy, że
,
przy założeniu, że B₀ = 1 (zbiór pusty posiada dokładnie jedną partycje). Ciąg {B_n}_n≥0 nazywamy ciągiem liczb Bella (lub ciągiem liczb eksponencjalnych).
Uwaga: Ilekroć poniżej będzie mowa o przypisywaniu ludzi do stolików lub do pokoi, to przyjmujemy, że:

• osoby sa rozróżnialne;
• stoliki są nierozróżnialne (identyczne).

Obserwacja
Korzystając ze znanych już interpretacji kombinatorycznych liczb można udowodnić nastepujące interpretacje kombinatoryczne liczb Bella:

1. B_n - liczba rozmieszczeń n różnych obiektów w co najwyżej n identycznych pudełkach.
2. B_n - liczba usadzeń n osób dookoła co najwyżej n stolików (gdy nieważny jest sposób usadzenia osób przy stoliku).
3. Liczba naturalna bedąca iloczynem n różnych liczb pierwszych może byż przedstawiona w postaci iloczynu różnych czynników na B_n sposobów.
4. B_n - liczba ciągów modelowych dla słów długości n.
5. B_n - liczba różnych schematów rymowych w strofie n-wersowej.
6. B_n - liczba permutacji zbioru {1, 2, ..., n} z określonym porządkiem na wszystkich cyklach.
7. Wiadomo, ze relacja równoważności dzieli zbiór, na którym jest określona na rozłączne i niepuste klasy abstrakcji. Wynika stąd i z Definicji 1, że B_n - liczba relacji równoważności na zbiorze n-elementowym.
8. σ-ciałem nad zbiorem skończonym A nazywamy rodzinę podzbiorów A zamkniętą ze względu na sumy przeliczalne i dopełnienia zbiorów. Każda partycja zbioru generuje σ-ciało (bierzemy wszystkie sumy i dopełnienia bloków partycji). Z kolei każdemu σ-ciału odpowiada dokładnie jedna partycja zbioru A. Jej bloki otrzymujemy biorąc dla każdego a∈A najmniejszy podzbiór zawierający a i należący do σ-ciała (otrzymane zbiory beda rozłączne). Z powyższego wynika, że liczba róznych σ-ciał nad zbiorem o n elementach jest równa liczbie wszystkich partycji tego zbioru, czyli B_n.

Rekurencja
Rozważmy usadzenia (n + 1) osób dookoła co najwyżej (n + 1) stolików (niektóre stoliki mogą być puste). Wyróżnijmy jedną osobę, np. ostatnią. Może ona siedzieć przy stoliku z r innymi osobami (r = 0, 1, 2, ..., n), które można wybrać na sposobów spośród innych osób. Wtedy pozostałe (n - r) osób może usiąść przy co najwyżej n stolikach na B_n-r sposobów. Stosując zasady: mnożenia i dodawania, mamy, że

Powyższe równanie rekurencyjne, wraz z warunkiem brzegowym: B₀ = 1 stanowi kolejna definicję ciągu liczb Bella i umożliwia wypisanie tablicy ich wartości.
Eksponencjalna funkcja tworząca
Funkcja ta dla ciągu liczb Bella jest postaci:

Jej zwarta postać możemy znaleźć korzystając z faktu, że

Sumując obie strony powyższego równania po k≥0 otrzymujemy

oraz

a stąd

Powyższe równanie możemy przedstawić w postaci:

Porównując współczynniki przy potęgach x otrzymujemy stąd wzór Dobińskiego:

Wzór ten jest podstawą do probabilistycznej interpretacji liczb Bella. Są one mianowicie momentami zwykłymi rozkładu Poissona z parametrem λ=1.

Liczby Catalana
Definicja
Liczbami tymi nazywamy szczególny ciąg liczbowy, mający zastosowanie w różnych aspektach kombinatoryki. Nazwane zostały na cześć belgijskiego matematyka Eugene Charlesa Catalana (1814–1894). Bywają również nazywane liczbami Segnera, na cześć matematyka pochodzącego z Karpat Niemieckich, Jána Andreja Segnera (1704-1777).
Każdy n-ty wyraz ciągu określony jest wzorem jawnym:

Rekurencyjnie ciąg jest określony w następujący sposób:

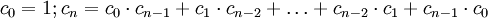
Początkowe wartości ciągu, poczynając od wyrazu zerowego, to: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
Własności
Liczby Catalana spełniają zależność:
.
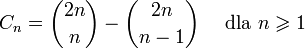W sposób oczywisty pokazuje to, iż każda liczba Catalana jest liczbą naturalną. Inną postacią wzoru rekurencyjnego (tym razem pierwszego stopnia) jest:
.
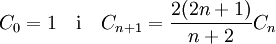Przybliżenie wartości n-tej liczby Catalana jest możliwe dzięki wzorowi Stirlinga na wartość silni i ma postać:

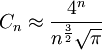
Znaczenie kombinatoryczne
Liczby Catalana posiadają wiele różnych interpretacji kombinatorycznych. Podane niżej stanowią jedynie przykłady zastosowań:

• Liczba dróg
Jeżeli rozważymy wszystkie łamane, zaczynające się w początku kartezjańskiego układu współrzędnych i kończące w (0,2n) dla każdego n=0,1,2,..., położone w jego I ćwiartce i złożone z pojedynczych odcinków o początku (x,y) i końcu w punkcie (x + 1,y + 1) lub (x + 1,y - 1) (gdzie x,y∈N), to ich liczba będzie wyrażona n-tą liczba Catalana.
• Liczba rozmieszczeń nawiasów
Poprzez ∗ rozumiemy pewne działanie dwuargumentowe. Dla n-argumentów liczba c_n-1 wyraża liczbę sposobów, na które można rozmieścić nawiasy w takim wyrażeniu, czyli - dla działania niełącznego - maksymalną liczbę wyników, które można uzyskać. Przykładowo, dla trzech argumentów x₁,x₂,x₃ otrzymać można (x₁∗x₂)∗x₃ lub x₁∗(x₂∗x₃), co odpowiada c_3-1 = c₂ = 2.
• Liczba drzew binarnych
c_n jest równa liczbie różnych ukorzenionych drzew binarnych o n + 1 liściach.
• Liczba monotonicznych dróg
Jeżeli rozpatrzymy wszystkie możliwe drogi w kwadracie (n x n) z dolnego lewego wierzchołka do górnego prawego, tak, by nigdy nie przekroczyć przekątnej łączącej te wierzchołki i były monotoniczne, łatwo jest zauważyć, że wyrażają się one n-tą liczbą Catalana. Odpowiada to liczbie monotonicznych funkcji f z 1,2,...,n w 1,2,...,n takich, by k≥f(k), k∈1,2,...,n

• Liczba podziałów na trójkąty
Liczba c_n wyraża liczbę sposobów podziału wielokąta wypukłego, mającego n + 2 krawędzie, na różne trójkąty przy pomocy przekątnych.

Dowód wzoru jawnego
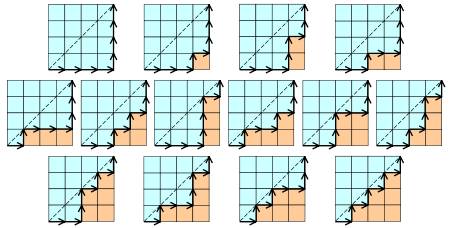
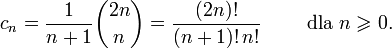Dowód wzoru można otrzymać na wiele sposobów i zależnie od różnych interpretacji liczb Catalana. Przyjmując, że rozpatrujemy przypadek liczby dróg z punktu (0,0) do (0,2n) i przy założeniu c₀=1 otrzymamy:
c₁=1 – bowiem do punktu (0,2) prowadzi jedna tylko droga,
c₂=2=c₀⋅c₁+c₁⋅c₀ – ponieważ do punktu (0,2) prowadzi jedna droga c₁, zaś z tego punktu do (0,4) można przejść zgodnie z założonymi możliwościami wyboru kolejnego odcinka składowego na jeden sposób.
Rozważmy teraz pewne przesunięcie układu współrzędnych tak, by punkt (1,1) stał się środkiem nowego układu współrzędnych – wówczas do punktu (1,3) prowadzi tyle samo dróg, co z punktu (0,0) do (0,2), zaś z (1,3) wykonując ruch zgodnie z założeniami można przejść na jeden sposób do punktu (0,4).
Postępując dalej analogicznie, otrzymamy:
.
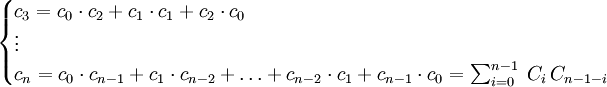Aby otrzymać wzór jawny, którym określony jest ciąg, można użyć techniki funkcji tworzących ciągu.
Niech C(x)=c0+c1⋅x+c2⋅x2... będzie funkcją tworzącą tego ciągu. Wówczas:


,
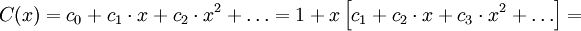
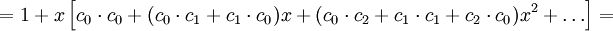
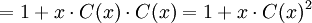co wynika z definicji operacji mnożenia funkcji tworzących. Mamy więc


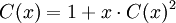
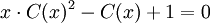
Rozwiązując to równanie, po przyjęciu za szukaną zmienną C(x) otrzymujemy:

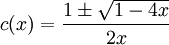
Ponieważ
,
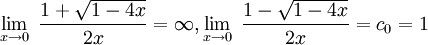to rozpatrujemy jedynie pierwiastek
.
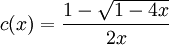Korzystając z uogólnionego na liczby rzeczywiste symbolu Newtona oraz jego własności okazuje się, że

.
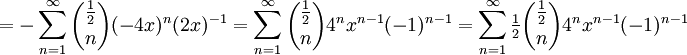Po zmianie granic sumowania otrzymujemy
.
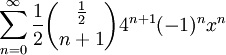Z własności funkcji tworzących wiemy, że n-ty wyraz ciągu jest równy współczynnikowi przy n-tej potędze x, czyli;


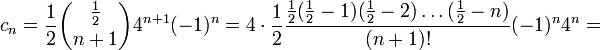
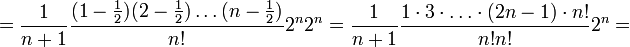
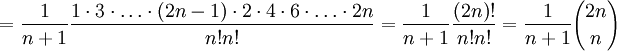
Historia
Liczby te zostały po raz pierwszy wprowadzone przez Leonarda Eulera w XVIII wieku, który badał liczbę podziałów wielokątów na trójkąty. Zostały nazwane na cześć Eugene Charlesa Catalana, który rozważał je jako liczbę sposobów rozmieszczeń nawiasów.

Liczby Stirlinga
Definicja
Są to dwa szczególne ciągi liczbowe analizowane przez Jamesa Stirlinga (1692-1770, szkocki matematyk).
I rodzaju
Opisują liczbę sposobów na rozmieszczenie n liczb w k cyklach, oznaczane są symbolem:

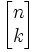
Który czyta się "k cykli n". Spełniają one związek rekurencyjny postaci:

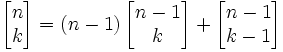
przy założeniach

Przyjmuje się, że jeżeli k > n, to

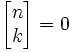
Niekiedy liczby Stirlinga pierwszego rodzaju są oznaczane innym symbolem:

Czasami przyjmuje się także naprzemienne, dodatnie i ujemne wartości liczb Stirlinga pierwszego rodzaju, co ma uzasadnienie przy wzorach na potęgi kroczące. W przyjętej tu konwencji liczby Stirlinga pierwszego rodzaju są zawsze nieujemne.

• Pochodzenie wzoru rekurencyjnego
Przyjmując za znaczenie liczb Stirlinga pierwszego rodzaju ilość rozmieszczeń n–liczb w k–cyklach, łatwo jest pokazać pochodzenie rekurencyjnej zależności między nimi. Wystarczy wybrać dowolną liczbę i rozpatrzyć ilość pozostałych cykli. Jeżeli ta liczba była w cyklu, składającym się z jednego elementu, to pozostałe n-1–liczb jest rozmieszczonych w k-1–cyklach, zaś dodanie jednej cyfry następuje w jeden sposób, poprzez stworzenie nowego cyklu. Jeżeli liczba była w liczniejszym cyklu, to pozostałe n-1–liczb jest rozmieszczonych w k–cyklach, zaś dodatkową liczbę można wstawić do dowolnego cyklu w dowolny sposób, czyli "obok" każdej liczby, a liczb jest n-1, co oznacza n-1–sposobów umieszczenia liczby w tym przypadku. Rekurencyjna zależność jest sumą obu przypadków. Warto przy tym zauważyć, że zbiór n–liczb można ustawić w 0 cykli na 0 sposobów, oraz 1 liczbę w 1 cyklu na 1 sposób.
• Potęgi kroczące
Liczby Stirlinga pierwszego rodzaju bywają także definiowane jako współczynniki, występujące przy zamianie potęg malejących (silni dolnej) na zwyczajne potęgi:

Przy zamianie normalnych potęg na potęgi rosnące (silnię górną) występuje zależność:

• Trójkąt liczbowy
Liczby Stirlinga I rodzaju tworzą trójkąt liczbowy podobny do trójkąta Pascala.

II rodzaju
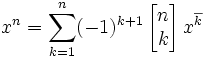
Opisują liczbę sposobów podziału zbioru n elementowego na k niepustych podzbiorów, oznaczane są symbolem:

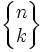
który czyta się "k podzbiorów n". Spełniają one związek rekurencyjny postaci:

przy założeniach

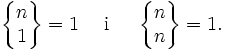
Przyjmuje się, że jeżeli k > n, to

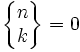
Niekiedy liczby Stirlinga drugiego rodzaju zapisywane są w inny sposób:

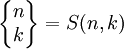
Liczby Stirlinga drugiego rodzaju są zawsze nieujemne.

• Potęgi kroczące
Niekiedy liczby Stirlinga drugiego rodzaju są definiowane jako współczynniki, występujące przy zamianie normalnych potęg na potęgi malejące (silnię dolną). Zachodzi wówczas zależność:

• Pochodzenie wzoru rekurencyjnego
Przyjmując za znaczenie liczb Stirlinga drugiego rodzaju ilość sposobów podziału zbioru n–elementowego na k–podzbiorów niepustych, łatwo jest uzasadnić rekurencyjną zależność. Rozpatrzymy zbiór n–liczb, i wybierzmy jedną z nich. Jeżeli ta liczba stanowiła jednoelementowy podzbiór, to pozostałe n-1–liczb będzie podzielone na k-1–podzbiorów, zaś jedną liczbę można dodać na jeden sposób, jako kolejny podzbiór. Jeżeli liczba była elementem liczniejszego podzbioru, to pozostałe n-1–liczb zostało podzielone na k–podzbiorów, zaś dodatkową liczbę można dołączyć do każdego z podzbiorów, których jest k. Można to więc w tym przypadku zrobić na dokładnie k–sposobów. Rekurencyjna zależność jest sumą obu przypadków. Warto przy tym zauważyć, że zbiór n–liczb można podzielić na 1 podzbiór na 1 sposób, a także na n–podzbiorów na 1 sposób.
• Trójkąt liczbowy

Własności

1. 
2. 
3. 
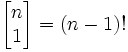
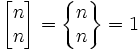
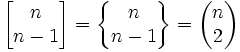
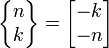4. - (prawo dualności)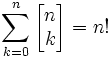
5. 
6. Z wzorów, pokazujących zależności między potęgami kroczącymi a normalnymi potęgami wynikają następujące zależności:

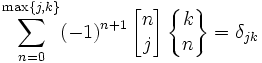
oraz

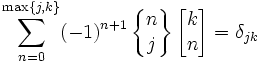
gdzie γ_jk to delta Kroneckera, j,k≥0.

Liczby Eulera
Definicja
Liczby Eulera - dwa ciągi liczbowe badane przez Leonarda Eulera (1707-1783, szwajcarski matematyk i fizyk).
I rzędu
Opisują ile jest permutacji n-elementowego zbioru posiadających k wzniesień, tzn. k pozycji, dla których π_j>π_j+1. Symbolem dla liczb Eulera I rodzaju jest:

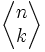
Liczby te spełniają wzór rekurencyjny postaci:

Z warunkami brzegowymi

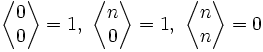
• Trójkąt liczbowy

• Własności

II rzędu
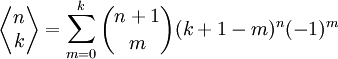
Liczby te są oznaczane jako:

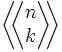
spełniają równanie rekurencyjne postaci:

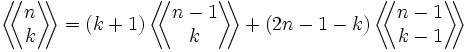
Z warunkami brzegowymi

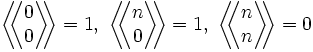
• Trójkąt liczbowy

Poprzednia Następna