Zagadnienia teorii grafów
Kolorowanie grafów
- Wprowadzenie Kolorowanie grafu polega w ogólności na przypisaniu określonym elementom składowym grafu (najczęściej wierzchołkom, rzadziej krawędziom lub ścianom) wybranych kolorów według ściśle określonych reguł. Klasyczne (czyli wierzchołkowe) kolorowanie grafu jest związane z przypisaniem wszystkim wierzchołkom w grafie jednej z wybranych barw w ten sposób, aby żadne dwa sąsiednie wierzchołki nie miały tego samego koloru. Innymi słowy, pewne pokolorowanie wierzchołkowe jest poprawne (legalne, dozwolone) wtedy, gdy końcom żadnej krawędzi nie przypisano tego samego koloru.
- Podstawowe definicje - Klasyczne (wierzchołkowe) kolorowanie grafu - przyporządkowywanie wierzchołkom grafu liczb naturalnych w taki sposób, aby końce żadnej krawędzi nie miały przypisanej tej samej liczby. Ze względów historycznych oraz dla lepszego zobrazowania problemu mówi się o kolorowaniu, przy czym różnym kolorom odpowiadają różne liczby.
- Algorytmy kolorowania grafów Ze względu na bardzo szerokie zastosowania, kolorowanie grafów jest przedmiotem rozległych badań. Problem znalezienia optymalnego pokolorowania, a także znalezienia liczby chromatycznej jest NP-trudny. Z tego względu do kolorowania dużych grafów nadają się jedynie algorytmy przybliżone.
- Twierdzenie o czterech barwach Twierdzenie o czterech barwach to jeden z najsłynniejszych problemów matematycznych. Twierdzenie to głosi, że dla każdego skończonego grafu planarnego (V, E) istnieje funkcja
- Pokolorowaniem wierzchołków grafu nazywamy jedno konkretne przyporządkowanie kolorów wierzchołkom. Pokolorowanie jest legalne (dozwolone), gdy końcom żadnej krawędzi nie przyporządkowano tego samego koloru.
- Optymalnym pokolorowaniem danego grafu nazywamy legalne pokolorowanie zawierające najmniejszą możliwą liczbę kolorów.
- Liczbą chromatyczną grafu G nazywamy liczbę X(G) równą najmniejszej możliwej liczbie kolorów potrzebnych do legalnego pokolorowania wierzchołków grafu G.
- Algorytm LF (largest first)
Kolorowanie grafu za pomocą algorytmu LF można opisać następująco:
1. Uporządkuj wierzchołki grafu malejąco według ich stopni (liczby krawędzi z nich wychodzących).
2. Koloruj wierzchołki zachłannie, zgodnie z ustaloną wcześniej kolejnością (zaczynając od wierzchołka o największym stopniu).
Algorytm LF jest algorytmem statycznym, gdyż raz ustalona kolejność wierzchołków nie zmienia się w trakcie jego działania. Najmniejszym dość trudnym grafem jest ścieżka P6.
- Algorytm SL (smallest last)
Algorytm SL wygląda następująco:
1. Znajdź wierzchołek o minimalnym stopniu i usuń go z grafu.
2. Powtarzaj krok pierwszy tak długo, aż graf będzie pusty (zapamiętaj kolejność usuwanych wierzchołków).
3. Koloruj wierzchołki zachłannie, zgodnie z ustaloną wcześniej kolejnością (zaczynając od wierzchołków usuniętych później).
Algorytm SL jest statyczny, jego złożoność wynosi O(n + m), gdzie n - liczba wierzchołków, m - liczba krawędzi. - Algorytm SLF (saturated largest first)
Kolorowanie grafu przy pomocy algorytmu SLF polega na wykonaniu poniższych czynności:
dopóki istnieją nie pokolorowane wierzchołki wykonuj operacje:
{
znajdź wierzchołek o maksymalnym stopniu spośród wierzchołków o maksymalnym stopniu nasycenia pokoloruj znaleziony wierzchołek zachłannie
}
Stopniem nasycenia wierzchołka nazwiemy tu liczbę różnych kolorów sąsiednich z tym wierzchołkiem. Złożoność algorytmu SLF wynosi O(mlogn).
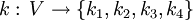 taka, że
taka, że 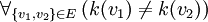 , czyli możliwe jest przypisanie każdemu z jego wierzchołków jednej z czterech liczb 1, 2, 3 i 4 w taki sposób, aby żadne sąsiednie wierzchołki nie miały przyporządkowanej tej samej liczby.
Sformułowanie równoważne (mniej ścisłe matematycznie, lecz bardziej przemawiające do wyobraźni): dowolną mapę polityczną na płaszczyźnie lub sferze można zabarwić czterema kolorami tak, aby każde dwa kraje mające wspólną granicę (a nie tylko wspólny wierzchołek) miały inne kolory (zakładamy, że wszystkie państwa są spójne terytorialnie).
Równoważność tych dwóch sformułowań łatwo zauważyć wyróżniając w każdym "kraju" "stolicę" i prowadząc drogi pomiędzy stolicami każdych dwóch sąsiednich krajów. Przechodzimy wówczas z mapy politycznej do grafu opisanego w pierwszym z powyższych sformułowań twierdzenia. Analogicznie można przejść w przeciwną stronę.
, czyli możliwe jest przypisanie każdemu z jego wierzchołków jednej z czterech liczb 1, 2, 3 i 4 w taki sposób, aby żadne sąsiednie wierzchołki nie miały przyporządkowanej tej samej liczby.
Sformułowanie równoważne (mniej ścisłe matematycznie, lecz bardziej przemawiające do wyobraźni): dowolną mapę polityczną na płaszczyźnie lub sferze można zabarwić czterema kolorami tak, aby każde dwa kraje mające wspólną granicę (a nie tylko wspólny wierzchołek) miały inne kolory (zakładamy, że wszystkie państwa są spójne terytorialnie).
Równoważność tych dwóch sformułowań łatwo zauważyć wyróżniając w każdym "kraju" "stolicę" i prowadząc drogi pomiędzy stolicami każdych dwóch sąsiednich krajów. Przechodzimy wówczas z mapy politycznej do grafu opisanego w pierwszym z powyższych sformułowań twierdzenia. Analogicznie można przejść w przeciwną stronę.
Uogólnienia na przypadek innych powierzchni
Istnieje uogólnienie twierdzenia o czterech barwach także dla grafów rozpiętych na powierzchniach topologicznych, które nie są homeomorficzne ze sferą lub płaszczyzną: dla każdej powierzchni liczba kolorów potrzebnych do zabarwienia dowolnej narysowanej na niej mapy politycznej tak, aby dwa sąsiednie kraje nie miały tej samej barwy, jest równa maksymalnej liczbie krajów na tej powierzchni, z których każdy dotyka każdego innego.
- Minimalne drzewo rozpinające (ang. MST, Minimum Spanning Tree ) jest to drzewo rozpinające danego grafu o najmniejszej z możliwych wag, tj. takie, że nie istnieje dla tego grafu inne drzewo rozpinające o mniejszej sumie wag krawędzi.
- Problem najkrótszej ścieżki Jest zagadnieniem szczególnie istotnym w informatyce. Polega on na znalezieniu w grafie ważonym najkrótszego połączenia pomiędzy danymi wierzchołkami. Szczególnymi przypadkami tego problemu są problem najkrótszej ścieżki od jednego wierzchołka do wszystkich innych oraz problem najkrótszej ścieżki pomiędzy wszystkimi parami wierzchołków. Okazuje się, że żeby znaleźć najkrótszą ścieżkę pomiędzy dwoma wierzchołkami grafu trzeba (w pesymistycznym przypadku) znaleźć najkrótsze ścieżki od wierzchołka wyjściowego do wszystkich innych wierzchołków. Problem najkrótszej ścieżki od jednego z wierzchołków do wszystkich innych można więc zobrazować jako problem znalezienia najkrótszej drogi pomiędzy dwoma miastami. W takim wypadku wierzchołkami grafu są skrzyżowania dróg, krawędziami – drogi, a wagi krawędzi odwzorowują długość danego odcinka drogowego. Do znalezienia najkrótszej ścieżki pomiędzy dwoma wierzchołkami zazwyczaj używane są algorytmy:
- Problem komiwojażera Patrz Zagadnienia przedstawiane jako problemy grafowe.
Definicja formalna
Dany jest graf ważony G(V, E, w), gdzie V - zbiór wierzchołków, E - zbiór krawędzi, w - funkcja przypisująca krawędzi Ei wagę (liczbę rzeczywistą lub całkowitą). Minimalnym drzewem rozpinającym nazywamy drzewo rozpinające, dla którego suma wag
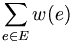
jest najmniejsza z możliwych. Dla niektórych grafów można wskazać wiele drzew rozpinających spełniających tę własność. Istnieją trzy deterministyczne algorytmy o złożoności liniowo-logarytmicznej znajdujące dla zadanego grafu minimalne drzewo rozpinające. Są to:
a) algorytm Borůvki (błędnie nazywany algorytmem Sollina)
b) algorytm Prima (nazywany też algorytmem Dijkstry-Prima)
Algorytm zachłanny wyznaczający tzw. minimalne drzewo rozpinające (MDR). Mając do dyspozycji graf nieskierowany i spójny, tzn. taki w którym krawędzie grafu nie mają ustalonego kierunku oraz dla każdych dwóch wierzchołków grafu istnieje droga pomiędzy nimi, algorytm oblicza podzbiór E' zbioru krawędzi E, dla którego graf nadal pozostaje spójny, ale suma kosztów wszystkich krawędzi zbioru E' ma najmniejszą możliwą wartość. Grafy zawierające dużo krawędzi, w których dwa te same wierzchołki połączone są np. trzema krawędziami lub pomiędzy dwoma wierzchołkami istnieje np. 5 różnych dróg długości 2, raczej nie są "lubiane" przez algorytmy i często przekształcenie takiego skomplikowanego grafu w graf mu równoważny pod względem zachowania możliwych połączeń przynosi znaczące korzyści.
c) algorytm Kruskala
Algorytm ten wyznacza minimalne drzewo rozpinające dla grafu nieskierowanego ważonego, o ile jest on spójny. Innymi słowy, znajduje drzewo zawierające wszystkie wierzchołki grafu, którego waga jest najmniejsza możliwa. Jest to przykład algorytmu zachłannego. Został on po raz pierwszy opublikowany przez Josepha Kruskala w 1956 roku.
a) Dijkstry (przy założeniu, że w grafie nie ma wag ujemnych) o pesymistycznej złożoności obliczeniowej
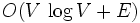 ,
,b)Bellmana-Forda o pesymistycznej złożoności obliczeniowej O(VE),
c) A*, używający heurystyki,
d) nienazwany (przy założeniu, że graf jest skierowany i nie ma cykli) o pesymistycznej złożoności obliczeniowej O(V + E),
gdzie V to liczba wierzchołków grafu, a E to liczba jego krawędzi.
Drugi szczególny przypadek problemu najkrótszej ścieżki występuje, gdy chcemy znaleźć najkrótsze ścieżki pomiędzy każdą parą wierzchołków. Oczywiście możliwe jest zrobienie tego dla każdego wierzchołka używając algorytmu znajdującego najkrótszą ścieżkę od jednego wierzchołka do wszystkich innych, jednak metoda ta okazuje się w praktyce niezbyt efektywna. Najkrótsze ścieżki pomiędzy wszystkimi wierzchołkami znajdują m.in. algorytmy:
a) nienazwany (wykorzystuje mnożenie macierzy) o pesymistycznej złożoności obliczeniowej
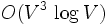
b) Floyda-Warshalla o pesymistycznej złożoności obliczeniowej O(Vdo3),
c) Johnsona o pesymistycznej złożoności obliczeniowej
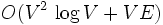
gdzie V to liczba wierzchołków.
-
Siecią przepływową G(V,E) nazywamy graf skierowany, w którym każda krawędź (u,v) należąca do zbioru krawędzi E ma nieujemną przepustowość
- Pojęcia: Przepływem w sieci G nazywamy każdą funkcję
- Problem maksymalnego przepływu: Jest to zagadnienie często spotykane w informatyce. Polega ono na znalezieniu dla danej sieci przepływowej takiego przepływu f, którego wartość jest maksymalna, gdzie wartość przepływu jest zdefiniowana jako łączny przepływ opuszczający źródło. Bardziej formalnie, dla danego przepływu f w sieci G=(V, E) o źródle s i ujściu t, jego wartość jest zdefiniowana następująco:
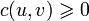 . W sieci wyrózniamy dwa wierzchołki: źródło s i ujście t.
. W sieci wyrózniamy dwa wierzchołki: źródło s i ujście t.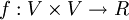 spełniającą warunki:
spełniającą warunki:a) warunek przepustowości: dla wszystkich krawędzi
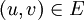 zachodzi
zachodzi 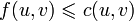 .
.b) warunek skośnej symetryczności: dla wszystkich krawędzi
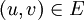 zachodzi f(u,v) = - f(v,u).
zachodzi f(u,v) = - f(v,u).c) warunek zachowania przepływu: dla każdego
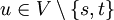 zachodzi
zachodzi 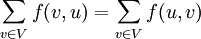 .
.Przepływ netto wartość f(u,v) przepływu z wierzchołka u do v.
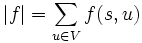
Istnieje też uogólnienie tego problemu, w którym sieć zawiera wiele źródeł i ujść. Można jednak w prosty sposób sprowadzić je do przedstawionej wersji: Dla sieci G=(V, E) zawierającej n źródeł
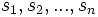 oraz m ujść
oraz m ujść 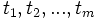 konstruujemy sieć
konstruujemy sieć 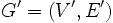 , gdzie:
, gdzie: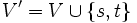
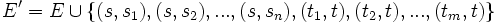
Ponadto:
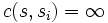 dla każdego
dla każdego 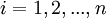
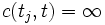 dla każdego
dla każdego 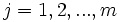
Innymi słowy, dodajemy do sieci G wierzchołek s połączony krawędziami o nieskończonej przepustowości ze wszystkimi źródłami oraz wierzchołek t połączony krawędziami o nieskończonej przepustowości ze wszystkimi ujściami. Wierzchołek s zwany jest superźródłem, zaś wierzchołek t - superujściem. Maksymalny przepływ można znaleźć m. in. za pomocą algorytmu Edmondsa-Karpa opartego na metodzie Forda-Fulkersona.
-
Klasyczne Liczby Ramseya związane są z kolorowaniem krawędzi grafu pełnego.
- Definicja Liczbą Ramseya
- Przykład Aby znaleźć np. wartość R(3,3) kolorujemy krawędzie grafów pełnych dwoma kolorami (np. czerwonym i niebieskim), szukając najmniejszego grafu pełnego, dla którego przy dowolnym kolorowaniu znajdziemy albo trójkąt czerwony albo trójkąt niebieski. Okazuje się, że R(3,3)=6. Ma to bardzo wygodną interpretację, mianowicie, w zbiorze 6 osób zawsze znajdziemy 3 osoby znające się wzajemnie lub 3 osoby które się nie znają.
- Wyznaczanie wartości Liczb Ramseya Okazuje się, że wyznaczenie wartości liczb Ramseya jest bardzo trudnym obliczeniowo zadaniem. Często mamy do dyspozycji bardzo dokładne ich oszacowania, a nie jesteśmy w stanie dokładnie określić ich wartości, mimo że nie są to wielkie liczby. Poniżej dotychczasowe osiągnięcia w tej dziedzinie:
- Nieklasyczne liczby Ramseya Klasyczne liczby Ramseya zdefiniowane są za pomocą kolorowania grafów pełnych w których poszukujemy monochromatycznych klik (czyli podgrafów pełnych). Pojęcie można jednak uogólnić na poszukiwania dowolnych podgrafów monochromatycznych.
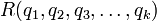 dla
dla 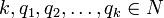 i
i 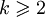 nazywamy najmniejszą liczbę n taką, że dla dowolnego k-pokolorowania krawędziowego n-wierzchołkowego grafu pełnego dla pewnego i,
nazywamy najmniejszą liczbę n taką, że dla dowolnego k-pokolorowania krawędziowego n-wierzchołkowego grafu pełnego dla pewnego i, 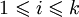 , w pokolorowanym grafie istnieje klika rozmiaru q(i), której wszystkie krawędzie są w kolorze i.
, w pokolorowanym grafie istnieje klika rozmiaru q(i), której wszystkie krawędzie są w kolorze i.
-
Skojarzeniem grafu nazywa się nie zawierający pętli podzbiór M krawędzi grafu E taki, że żadne dwie krawędzie w M nie są sąsiednie, tj. nie spotykają się w jednym wierzchołku.
Wierzchołki będące końcami krawędzi należących do M są M-nasycone. Wierzchołki nie będące końcami krawędzi należących do M są M-nienasycone.
Skojarzenie doskonałe to podzbiór M krawędzi grafu G, taki, że każdy wierzchołek G jest M-nasycony. Skojarzenie doskonałe jest zawsze skojarzeniem największym, tj. takim, że nie istnieje skojarzenie grafu G o większej liczbie krawędzi. Pary wierzchołków połączone bezpośrednio krawędzią należącą do M są skojarzone przez M. M-przemienna ścieżka to ścieżka ułożona naprzemiennie z krawędzi należących i nienależących do M.
- Definicja Izomorfizm grafów – Grafy G i F nazywamy izomorficznymi, jeżeli istnieje bijekcja zbioru wierzchołków grafu G na zbiór wierzchołków grafu F, która zachowuje strukturę grafu (krawędzie). Intuicyjnie oznacza to, że grafy G i F są tym samym grafem, jedynie poddanym jakiejś permutacji wierzchołków.
- Przykład Grafy znajdujące się na górze są izomorficzne względem siebie, bo są to cykle C5, a wszystkie cykle nieskierowane o tej samej liczbie wierzchołków są względem siebie izomorficzne. Izomorfizmem przekształcającym lewy graf na prawy jest funkcja dana przez:
- Rozstrzyganie izomorficzności Problem rozstrzygania izomorficzności dwóch grafów należy do klasy NP ale prawdopodobnie nie jest problemem NP zupełnym. Z drugiej strony nie są znane wielomianowe algorytmy deterministyczne, probabilistyczne ani kwantowe rozwiązujące ten problem. Nie wiadomo też czy problem należy do klasy co-NP.
f(a)=a, f(b)=d, f(c)=b, f(d)=e, f(e)=c.
Dla grafów dolnych należy zwrócić uwagę, że są to ścieżki o tej samej liczbie wierzchołków, ale funkcja przekształcająca izomorficznie lewy graf na prawy jest już inna:
f(b)=b, f(e)=a, f(c)=e, f(a)=d, f(d)=c.
Efektywne wielomianowe rozwiązania tego problemu znaleziono dla szczególnych klas grafów, między innymi:
a) grafów planarnych
b) grafów o ograniczonym stopniu
c) grafów przedziałowych
d) grafów permutacji
e) grafów wypukłych
Uogólnieniem tego problemu jest problem izomorfizmu podgrafu, o którym wiadomo że jest problemem NP zupełnym.
- Definicja Reprezentacja grafu to sposób zapisu grafu umożliwiający jego obróbkę z użyciem programów komputerowych. Dwa najpopularniejsze sposoby zapisu informatycznego grafów to macierz sąsiedztwa oraz listy sąsiedztwa.
- Reprezentacja przez macierz sąsiedztwa Macierz sąsiedztwa to dwuwymiarowa macierz, reprezentowana przez tablicę M o wymiarach [0..V] na [0..V], gdzie V to liczba wierzchołków grafu. Jeżeli pomiędzy wierzchołkami vi i vj jest krawędź to M[i][j]=1, w przeciwnym wypadku M[i][j]=0. Własności reprezentacji:
- Reprezentacja przez listy sąsiedztwa Zapamiętanie tablicy o rozmiarze V² jest dość kosztowne, zwłaszcza gdy bada się grafy rzadkie' tj. grafy o liczbie wierzchołków wielokrotnie przewyższającej ilość krawędzi. W praktyce wielokrotnie lista sąsiedztwa okazuje się efektywniejszą reprezentacją grafu. Korzysta się z list - struktury danych, która przechowuje różne wartości w komórkach zwanych węzłami. Tutaj w listach będziemy trzymać numery indeksów. Tworzy się tablicę wskaźników na puste listy o rozmiarze 0(n). Niech tablica nazywa się LS. Dla każdej krawędzi (vi,vj), do listy wskazywanej przez LS[i] dodaje się indeks wierzchołka vj. LS[i] wskazuje teraz na listę zawierającą indeksy wszystkich sąsiadów wierzchołka vi. Aby usunąć krawędź (vi,vj) wystarczy usunąć z listy LS[i] indeks vj, a z LS[j] indeks vi.
- Implementacja grafu w C++ (reprezentacja macierzowa) Realizacja obsługi grafu poprzez macierz jest dość prosta:
- Implementacja grafu w C++ (reprezentacja listowa) Definicja klasy CGraph jest niemal taka sama:
Niech G = < V,E > będzie grafem, V zbiorem wierzchołków, a E zbiorem krawędzi. Bez straty ogólności możemy nadać każdemu wierzchołkowi indeks
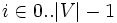 . Zbiór wierzchołków G:
. Zbiór wierzchołków G: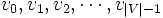
Sam wierzchołek najlepiej reprezentować za pomocą rekordu, klasy lub innych struktur danych. Jeżeli G miałby reprezentować strukturę pracowników firmy, definicja wierzchołka (pracownika) mogłaby wyglądać tak:
a) Macierz sąsiedztwa:
b)Wymagania pamięciowe: α( | V |²)
c) Dodanie nowej krawędzi: czas stały
d) Sprawdzenie czy dana krawędź istnieje: czas stały
e) Sprawdzenie stopnia danego wierzchołka: α( | V | )
f) Usunięcie krawędzi: czas stały
a) Wymagania pamięciowe: α( | E | )
b) Dodanie nowej krawędzi: czas stały
c) Sprawdzenie czy dana krawędź istnieje: α( | E | )
d) Sprawdzenie stopnia danego wierzchołka: α( | E | )
e) Usunięcie krawędzi: α( | E | )
Konstruktor rezerwuje pamięć na macierz sąsiedztwa i tworzy graf o V wierzchołkach i 0 krawędziach. Destruktor zwalnia pamięć.
Dodanie krawędzi, jeżeli graf jest prosty i krawędź już istnieje funkcja zwraca 0. Jeżeli graf nie jest skierowany symetryczna krawędź jest dodana.
Aby usunąć krawędź, należy sprawdzić czy takowa istnieje i w przypadku grafu prostego usunąć krawędź symetryczną.
Zliczanie sąsiadów wierzchołka v realizujemy przez zsumowanie wartości GMatrix[v][i],
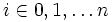 , tj. ilości krawędzi o końcu w wierzchołku v. Jeżeli obsługujemy graf skierowany funkcja Degree(v) zwróci ilość krawędzi wychodzących z v.
, tj. ilości krawędzi o końcu w wierzchołku v. Jeżeli obsługujemy graf skierowany funkcja Degree(v) zwróci ilość krawędzi wychodzących z v.Konstruktor rezerwuje pamięć na V elementową tablicę wskaźników na listy, oraz ustawia początkowe zawartości list na NULL (graf bez krawędzi).
Funkcja Search(v,u) przechodzi całą listę sąsiadów do napotkania węzła reprezentującego wierzchołek u, lub do końca listy, tj. węzła, którego wskaźnik next wskazuje na NULL;
Funkcja Delete(v,u) wywołuje funkcję Search(v,u), która w przypadku istnienia krawędzi (v,u) zapamiętuje wskaźniki odpowiednio na poprzedni i następny węzeł na liście. Jeżeli krawędź nie istnieje, Delete zwraca 0. Jeżeli istnieje, węzeł u jest usuwany z listy sąsiadów v, i odwrotnie.
Patrz Zagadnienia przedstawiane jako problemy grafowe.