Poprzednia Następna

Problem komiwojażera

• Opis
Problem komiwojażera (TSP - ang. traveling salesman problem) jest to zagadnienie z teorii grafów, polegające na znalezieniu minimalnego cyklu Hamiltona w pełnym grafie ważonym.
Nazwa pochodzi od typowej ilustracji problemu, przedstawiającej go z punktu widzenia wędrownego sprzedawcy (komiwojażera): dane jest n miast, które komiwojażer ma odwiedzić, oraz odległość pomiędzy każdą parą miast.
Symetryczny problem komiwojażera (STSP) polega na tym, że odległość pomiędzy miastami A i B jest zawsze taka sama. W asymetrycznym problemie komiwojażera (ATSP) odległość od miasta A do miasta B może być inna, niż odległość od miasta B do miasta A.
Rozwinięciem problemu komiwojażera jest problem marszrutyzacji.
• Przykład
Miasta: Kutno,Warszawa,Poznań,Kraków
Odległości:

Należy znaleźć najkrótszą trasę zaczynającą się np. z Kutna, przechodzącą jednokrotnie przez wszystkie pozostałe miasta i wracającą do Kutna.
Problem ten jest NP-trudny.
• Wersja decyzyjna
W wersji decyzyjnej problemu, danymi są graf i pewna liczba n, należy odpowiedzieć czy istnieje trasa komiwojażera krótsza od n.
Tak sformułowany problem jest NP-zupełny.

Problem chińskiego listonosza

• Opis
Problem chińskiego listonosza (ang. Chinese postman problem lub route inspection problem) – w teorii grafów zadanie znalezienia drogi zamkniętej (wracającej do wierzchołka początkowego), zawierającej każdą krawędź grafu co najmniej raz i mającej minimalny koszt (sumę wag krawędzi).
Dlaczego chińskiego ? Problem ten został sformułowany po raz pierwszy w języku teorii grafów przez chinskiego matematyka Mei Ku Kwana w 1962 roku.
Dlaczego listonosza ? W swojej pracy, listonosz wyrusza z poczty, dostarcza przesyłki adresatom, by na koncu powrócić na pocztę. Aby wykonać swoją pracę musi przejść po każdej ulicy w swoim rejonie co najmniej raz. Oczywiście chciałby, aby droga, którą przebędzie, była możliwie najkrótsza.
Złożoność obliczeniowa problemu uzależniona jest od rodzaju grafu, na którym jest on rozpatrywany. W przypadku grafów w całości skierowanych albo nieskierowanych jest to problem klasy P. W przypadku grafów mieszanych (częściowo skierowanych, częściowo nieskierowanych) problem zalicza się do klasy NP-zupełnych[1].
• Sformułowanie problemu
Rozważmy graf, którego krawędzie odpowiadają ulicom w rejonie, obsługiowanym przez listonosza. Wierzchołki to po prostu skrzyżowania ulic. Krawędziom nadajemy wagi, które oznaczają odległości między dwoma skrzyżowaniami. Znalezienie możliwie najkrótszej drogi, którą musi przejść listonosz sprowadza sie do znalezienia w tym grafie drogio minimalnej sumie wag krawędzi, która przechodzi przez każdą krawędź co najmniej raz.
Jeśli dany graf posiada cykl Eulera, to istnieje taka droga, która zaczyna i konczy sie w tym samym punkcie i wymaga przejścia po każdej ulicy dokładnie raz. Zauważmy, że ponieważ każdy cykl Eulera przechodzi raz przez każdą krawędź to suma wag krawędzi (długość drogi, którą musi przejść listonosz) jest zawsze taka sama (nie zależy od wierzchołka, w którym cykl ten zaczyna się i konczy). Rozwiązaniem jest więc dowolny cykl Eulera w tym grafie.
Jeśli graf nie posiada cyklu Eulera. W takim przypadku listonosz będzie zmuszony przejść niektórymi ulicami wielokrotnie. Rozwiązanie jest więc cyklem, w którym suma długości krawędzi wybranych więcej niż raz jest możliwie najmniejsza.
• Przykład
Na rysunku pokazany est układ ulic niedaleko Politechniki Warszawskiej. Załóżmy, że fragmenty tych pięciu ulic tworzą rejon listonosza.

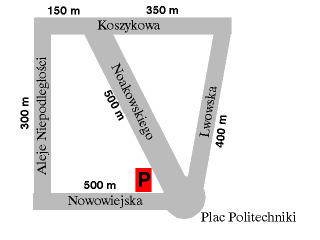
Obok nazw ulic umieszczone są odległości w metrach. Prostokąt oznaczony literą P oznacza miejsce, w którym umieściliśmy pocztę, na której pracuje 'nasz' listonosz. (Na marginesie: nazwy i układ ulic są prawdziwe, jednak podane odległości oraz umiejscowienie poczty nie odpowiadają rzeczywistości. Pocztę umieścilismy w miejscu, gdzie w rzeczywistości znajduje się Gmach Główny, w którym ma swoją siedzibę Wydział MiNI. I niestety nie ma w tym budynku poczty.) Oto jak wygląda graf odpowiadający danemu układowi ulic. Zauważmy, że graf ten nie ma cyklu Eulera ponieważ posiada dwa wierzchołki, z których wychodzi nieparzysta liczba krawędzi. Na rysunku zaznaczono również rozwiązanie czyli optymalną trasę listonosza.

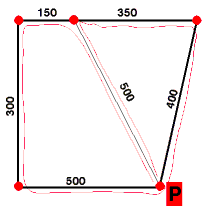
Zwróćmy uwagę, że listonosz musi przejść dwukrotnie tylko ulicę Noakowskiego, zaś pozostałe ulice dokładnie raz. Powyższa droga jest najkrótszą z możliwych ponieważ odcinek, po którym przechodzi dwukrotnie liczy tylko 500 metrów i nie istnieje trasa spełniająca zadane warunki o krótszym odcinku, który listonosz musi pokonać więcej niż raz.

Problem marszrutyzacji

• Opis
Problem marszrutyzacji (ang. Vehicle Routing Problem (VRP)) – problem decyzyjny polegający na wyznaczeniu optymalnych tras przewozowych dla pewnej ściśle określonej ilości środków transportu, której zadaniem jest obsłużenie zbioru klientów znajdujących się w różnych punktach przy zachowaniu ograniczeń. Kryterium optymalizacji jest całkowity koszt transportu (wyrażony odległościowo, cenowo lub czasowo). Istnieją również rozwinięcia problemu uwzględniające więcej, niż jedno kryterium optymalizacji[1]. Problem marszrutyzacji należy do podstawowej problematyki zarządzania operacyjnego flotą środków transportu (rzadziej zarządzania na wyższym szczeblu).
Problem ten jest rozwinięciem takich problemów jak:
- problem komiwojażera (traveling salesman problem),
- problem domokrążnego kupca (traveling purchaser problem),
- problem chińskiego listonosza (chinese postman problem),
oraz zaliczany jest do problemów NP-trudnych. Z tego względu zazwyczaj jest rozwiązywany przy pomocy metod heurystycznych. Algorytmy dokładne mogą być wykorzystywane tylko dla problemów o stosunkowo niewielkiej ilości klientów (do 135).
Problem został po raz pierwszy zaprezentowany przez G.B. Dantziga oraz R.H. Ramser'a w 1959 roku w pracy The Truck Dispatching Problem opublikowanej na łamach Management Science.
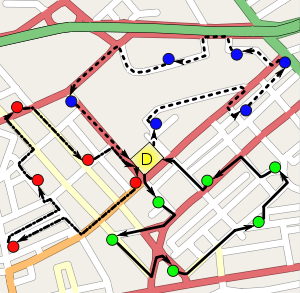
• Graficzna prezentacja rozwiązania
Graficzna prezentacja rozwiązania problemu marszrutyzacji (nieoptymalnego!). Zostały wyznaczone trzy marszruty (linie: ciągła, przerywana i kropkowana), które swój punkt początkowy i końcowy mają w bazie (żółty prostokąt "D") oraz przebiegają przez wszystkie punkty pośrednie (klientów - czerwone, zielone i niebieskie punkty).

• Klasyczne ujęcie problemu
W klasycznym ujęciu problem sformułowany jest w postaci grafu nieskierowanego Γ = (Ψ,ε), gdzie Ψ oznacza zbiór wierzchołków, do których przypisane jest zapotrzebowanie, natomiast ε zbiór krawędzi, do których przypisane są koszty przewozu ewentualnie czas lub długość trasy.
Minimalizowana jest funkcja

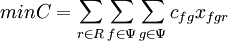
gdzie:
r – pojazd należący do zbioru jednorodnych (identycznych) pojazdów R
f, g – wierzchołki pomiędzy, którymi odbywa się przewóz
c_fg – koszt przewozu pomiędzy wierzchołkami f i g
x_fgr – zmienna binarna określająca, czy pomiędzy wierzchołkami f i g pojazd r wykonuje przewóz.
Warunkami ograniczającymi są:
- Występowanie tylko jednej bazy początkowej i końcowej (miejsca, z którego pojazdy rozpoczynają/kończą przewóz), z której/do której wyjeżdża dokładnie jeden pojazd r. W przypadku wierzchołków pośrednich ilość pojazdów wjeżdżających jest równa ilości pojazdów wyjeżdżających.
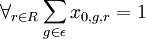– dla bazy początkowej
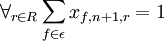– dla bazy końcowej
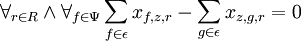– dla wierzchołków pośrednich
W przypadku, gdy istnieje połączenie pomiędzy punktami 0 oraz n+1 to dopuszczalne są puste drogi - Przypisanie każdemu klientowi dokładnie jednego pojazdu, który zaspokaja jego zapotrzebowanie (dostawy są niedzielone).
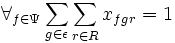– warunek przypisania dokładnie jednego pojazdu
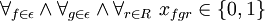– warunek niedzielonych dostaw
• Przykładowe rozwinięcia problemu
W rozwinięciach klasycznego problemu marszrutyzacji występować mogą dodatkowe ograniczenia. Przykładowo: - Warunek nieprzekroczenia pojemności poszczególnych środków transportu (problem CVRP).

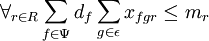
gdzie:
d_f – popyt przypisany do danego klienta
m_r – pojemność pojazdów
- Ograniczenia czasowe w problemach z oknami czasowymi (pojazd nie przybędzie do określonego wierzchołka przed wykonaniem poprzednich zadań w węzłach poprzedzających)

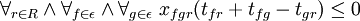
gdzie:
t_fr – czas rozpoczęcia obsługi klienta f
t_fg – czas przejazdu pomiędzy f, a g
t_gr – czas rozpoczęcia obsługi klienta g
• Rozwinięcia problemu
W literaturze występują również rozwinięcia klasycznego problemu marszrutyzacji. Należą do nich m.in.:
- Problemy uwzględniające niesymetryczność kosztów przewozu pomiędzy wierzchołkami
- Problemy uwzględniające niehomogeniczność taboru
- Problemy uwzględniające przejazdy drobnicowe (Less Than Truckload)
- Problemy uwzględniające ograniczenie maksymalnej długości trasy
- Problemy umożliwiające ustalenie baz (jednej lub kilku), w których pojazdy zaczynają i kończą podróż (Multiple Depot VRP)
- Problemy umożliwiające dodanie baz pomocniczych (VRP with Satellite Facilities)
- Problemy umożliwiające ustalenie częstotliwości odbioru/dostawy ładunku
- Problemy umożliwiające uwzględnienie okien czasowych (VRP with Time Windows) odbioru/wysłania towaru.
- Problemy wiążące problem marszrutyzacji z problemem kontroli zapasów u klientów
- Problemy uwzględniające możliwość obsługi jednego klienta przez kilka pojazdów (Split Delivery VRP)
- Problemy w których kosztowa funkcja celu zastąpiona została innymi parametrami (np. czas wykonania zleceń, długość tras, ilość przewiezionego ładunku)
- Problemy umożliwiające zdefiniowanie kolejności odwiedzania poszczególnych miejsc oraz opcjonalnego odwiedzania niektórych punktów.
- Problemy uwzględniające możliwości zwrotów i wysyłki towarów przez klientów (VRP with Backhauls oraz VRP with Pick-Up and Delivering – problem rozwózkowo-zwózkowy)
- Problemy, w których warunki zostały ujęte stochastycznie (Stochastic VRP)
• Problem marszrutyzacji a problemy "capacitated arc routing"
W problemie marszrutyzacji klienci stwarzający popyt na transport są zlokalizowani w wierzchołkach grafu. W rzeczywistości problem ten ma zastosowanie np. w tradycyjnych firmach przewozowych. Problemy, w których popyt jest zlokalizowany na krawędziach grafu należą do grupy problemów arc routing, a odpowiednikiem problemu marszrutyzacji jest problem CARP. W rzeczywistości sytuacje takie występują przykładowo podczas opracowywania marszrut dla zamiatarek drogowych, śmieciarek, czy też pługopiaskarek.

Problem kojarzenia małżeństw

• Opis
Twierdzenie o kojarzeniu małżeństw (twierdzenie Halla) – przypisywane zazwyczaj Philipowi Hallowi twierdzenie dotyczące istnienia pełnego skojarzenia grafu dwudzielnego, sformułowane w roku 1935. Jest ono często ilustrowane poprzez przedstawienie następującego problemu:
Mamy dwie grupy - dziewcząt i chłopców, oraz pewną sieć znajomości, to znaczy wiemy, których chłopców z tej grupy zna każda z dziewczyn. Kiedy zachodzi sytuacja, w której każdej dziewczynie można przyporządkować jednego kandydata na męża? Oczywiście, tacy kandydaci nie mogą się powtarzać.
Rozwiązanie tak postawionego problemu nosi nazwę twierdzenia o kojarzeniu małżeństw.
Okazuje się, że warunkiem koniecznym i warunkiem wystarczającym na to, by istniało takie skojarzenie par, jest to, by każda podgrupa dziewcząt, licząca k osób, znała co najmniej k chłopców.
• Twierdzenie
Twierdzenie można przełożyć na język matematyki na kilka sposobów:
1. Wersja dla grafów
Niech G=(V, E) będzie grafem, i niech 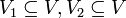będą rozłącznymi podzbiorami zbioru wierzchołków, 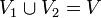, takimi, że jeśli e jest dowolną krawędzią grafu i e={v, u}, to spełniony jest warunek
,
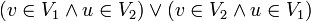czyli graf G jest grafem dwudzielnym. Wówczas w tym grafie istnieje skojarzenie, którego krawędzie są incydentne ze wszystkimi wierzchołkami z V₁ wtedy i tylko wtedy, gdy dla każdego podzbioru wierzchołków 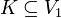zachodzi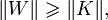

gdzie:

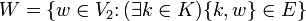
to zbiór wierzchołków z V₂ połączonych krawędzią z którymkolwiek wierzchołkiem z K
||X|| to moc zbioru X
Jeżeli ||K||=||W|| to takie skojarzenie jest pełne (doskonałe).
2. Wersja dla transwersal
Twierdzenie Halla dla transwersal mówi, że dla rodziny R istnieje transwersala wtedy i tylko wtedy, gdy dla każdej k-elementowej podrodziny rodziny R mnogościowa suma wszystkich składowych tej podrodziny ma k lub więcej elementów.

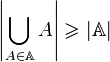
dla każdego .
• Dowód
Podany dowód jest sformułowany dla transwersal, dla grafów jest on analogiczny.
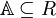Oczywiste jest, iż jest to warunek konieczny, bowiem gdyby nie był on spełniony i suma mnogościowa pewnej elementów pewnej rodziny zbiorów miała mniej niż k-elementów, to nie byłoby możliwe wybranie k-elementowego podzbioru złożonego z elementów tej sumy.
Wystarczalność warunku można udowodnić, korzystając z indukcji matematycznej. Przez n oznaczę ilość podzbiorów zbioru 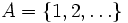. Zauważmy, że dla n = 1 twierdzenie jest prawdziwe, bowiem można wybrać jeden dowolny element z S₁. Niech n > 1. Zakładamy, że twierdzenie jest prawdziwe dla .
Jeżeli dla danego n mnogościowa suma zbiorów 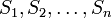ma więcej niż n elementów, to twierdzenie jest prawdziwe, wystarcz bowiem wybrać dowolny element k zbioru 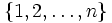, utworzyć transwersalę dla n-1-elementowej rodziny zbiorów 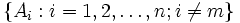(co jest możliwe na mocy założenia indukcyjnego) oraz dołączyć do niej element k.
W przeciwnym wypadku istnieje pewien podzbiór J (właściwy) zbioru 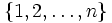taki, że suma mnogościowa wszystkich elementów zbiorów 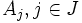jest równa ilości elementów zbioru J. Wybierzmy teraz transwersalę dla rodziny 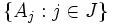oraz rodziny 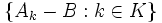, gdzie , zaś 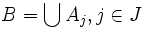. Dla obu rodzin na mocy założenia indukcyjnego istnieją transwersale, i są one rozłączne, co wynika z powyższych warunków. Poszukiwaną transwersalą jest więc zbiór, będący sumą tych transwersal.

Poprzednia Następna